Experiment of The Month
Cosmic Ray Muons and Einstein's Special Relativity
The MU Physics Department does not claim to have invented these labs. The exercise below has been done many times in many places, with many variations. Two references are given at the bottom of the page. We believe that each performance of the lab will be unique; in each nature will reveal a slightly different face to the observer.
Go to a workshop on Einstein's Special Relativity.
In this demonstration exercise, we detect and identify cosmic ray muons. Classical analysis of their lifetime and the rate at which they arrive
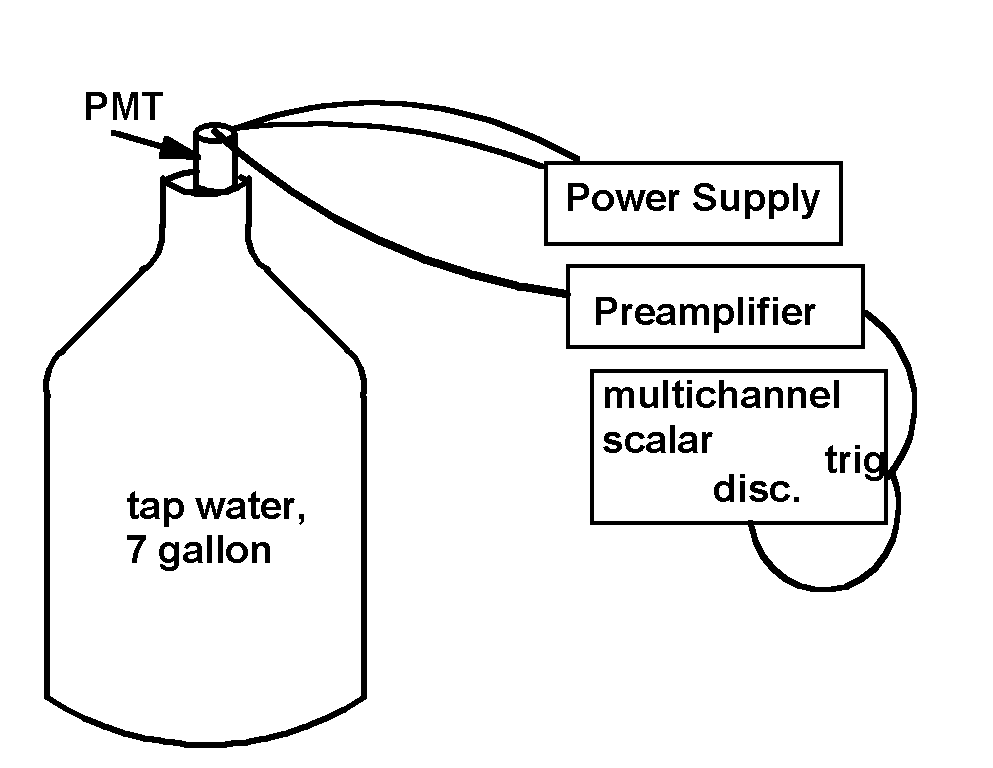
The basic experimental set up is shown in the figure. When the signal from the preamplifier is sent to an oscilloscope, pulses are displayed on the oscilloscope. The rate of occurrence of the pulses increases when a small radioactive source is placed near the jug. We associate the light flashes detected by the photomultiplier with particles passing through the water, ionizing atoms as they go.
In operation, the pulses travel first to the trigger input of the multichannel
If a second pulse arrives during that
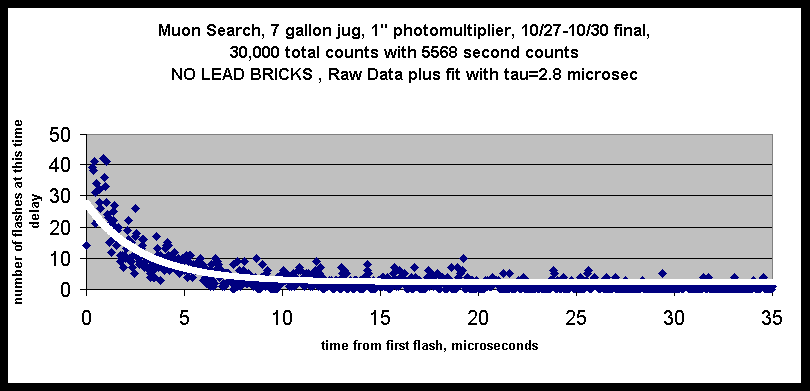
The intent is to detect first the light flash that occurs when a muon arrives in the jug, and then to detect the flash Associated with the muon decay. Most muons do not decay in the jug, but enough do for us to make a measurement. Accelerator experiments show that the muons decay with a characteristic time of about 2 microseconds. The decay is exponential so that if a population of muons is observed at any particular time, we know that 2 microseconds later only about 1/3 of that population will remain.
The probability of decay for a muon observed at t=0 is exponential with the same characteristic time as the population. Thus we can expect 2/3 of the decays to occur within about 2 microseconds of the initial pulse. This result is independent of the previous history of the
The figures at the right
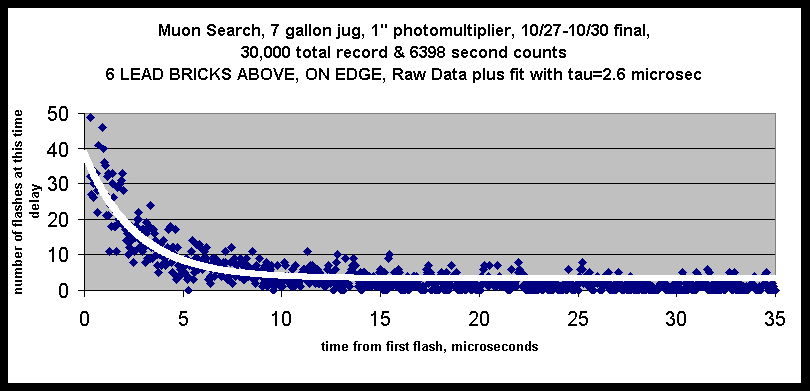
This result is consistent with idea that most muons are too energetic(1) to be stopped by the water, and so will not stay in the jug long enough to decay and be detected. The lead bricks are supposed to slow down some of those fast muons, make them "stoppable," in the water, and create more observed muon decays. The importance of the argument is that it is evidence for the muons arriving from above, and not from the earth.
If the results shown above are taken as typical, then they do indicate that the source of muons is from above. (They remain atypical at present, as we continue to optimize our choice of electronic thresholds.) If the muons come from above, the obvious next question is how far above. Since they live only a few microseconds, the cannot come directly from stars or other distant objects.
The proposed model is that they are created at the top of the atmosphere by collisions of cosmic ray "primary" particles. If those particles are, for example, protons, then they live long enough to make the trip from distant parts of the universe. If the muons are formed at the top of the atmosphere, then they must travel about 10 kilometers down in order to reach our detector. The question of whether they live long enough to get here still arises.
If they travel at the speed of light, it will take a muon about 30 microseconds to reach earth. This is 15 times the muon characteristic decay time. This means that only about 1 muon survives at the earth surface for every 10 million that start out at the top of the atmosphere.
The
We see about one flash every 30
Thus in a column above us, 3 meters square (and 10,000 meters high) we would expect to see 10 million times that much light, from all the muons that decayed before reaching us. Each 3 square meter patch above us should radiate about 1 microwatt of light.
The planet Venus sends about 1 microwatt of light energy to a square meter of earth. This calculation indicates that we should be seeing about "one Venus worth" of light from
It does not.
The resolution of this contradiction is found in the special theory of relativity. When we observe a moving object which carries a clock, we see the clock running slow. If we could watch a muon coming down from the top of the atmosphere we would see it's "clock run slow."
Since for us that clock runs slow, we observe many more muons surviving at the surface of the earth than we would have expected. Our estimate of one in 10 million being able to reach the earth is
In this way, the muon observations disagree with classical mechanics and agree with Einstein's special theory of relativity.
Students or teachers who want to work with real muon detector data may contact Dr. Dooley at the Physics Department, Millersville University. Jwdooley@aol.com.
(1)A.O. Weissenberg, Muons, John Wiley & Sons (1967), p316.
It has the most complete discussion of the behavior of cosmic ray muons and an effective list of references.
A good list of references is also available at
http://www.physics.umd.edu/studinfo/courses/gradlab/glhb/muon.html