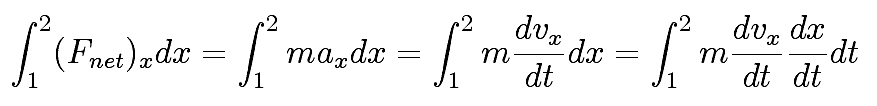Experiment of The Month
Calculus in Physics
As Galileo (a gifted experimenter) promised us, mathematics is a language.
Among the stories which can be told in this language are physics stories.
(Novelists often speak of a story finishing itself,
or of a character "taking over" a story. )
If you begin a physics story carefully in this language,
the story will often finish itself, with no help from you.
Millersville physics is old-fashioned in some ways. We teach no virtual laboratories, for example. (In fact only one virtual lab is currently taught at Millersville; it is in the Earth Sciences Department.) Our
When Newton invented calculus, he invented the language that has been used for physics ever since. Since our students have demonstrated skill in calculus, we are able to use the proper mathematical language from the start in Physics 231. This issue of "experiment of the month" is a catalog of some of the ways in which calculus is used in our introductory physics course. The examples show that calculus is not simply a "hurdle" which must be cleared before taking physics. For us, calculus is a "step up" to a higher level of performance and understanding.
(Picture at http://www.er.uqam.ca/nobel/r14310/Ptolemy/Images/Galileo/Leoni/Louvre/completNB.jpg)
Error Propagation
The experience which may bring calculus most directly to physical events is the propagation of experimental error. We follow the development shown at http://mathworld.wolfram.com/ErrorPropagation.html
Suppose that we take measurements of parameters x
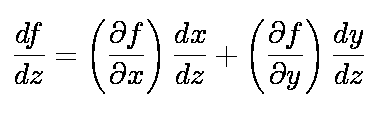
Students know the chain rule, although most are not familiar with the partial derivative notation. We next use "physics license" to "multiply through by
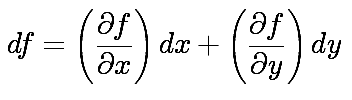
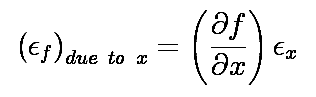
A similar expression is true for the error due to the error in y. This is a natural point to notice that we can use this differential method to determine which measurement deserves the most attention if we want to reduce the error in
The fact that the derivative can be either positive or negative requires attention. If there were only one parameter, x, then we could just take the absolute value of the derivative. Since the x value can vary + or - the error in x from the best value, the sign of the derivative does not matter.
If there are several parameters, we must find a rule for combining the errors, in the face of the likelihood that some derivatives are negative and some are positive. Simply adding can lead to non-representative conclusions, such as an error in f that is zero.
The simpler way to deal with the negatives is less supportable. We call it the "worst case" estimate of error. For the worst case, we simply add the magnitudes of each error contribution. The statistically valid method is to calculate the square root of the sum of the squares of all error contributions.
The error discussion was extended because it gives students a reason to use calculus in the laboratory, calculating the derivatives for themselves. Comparing measurement errors with function errors makes concrete a basic concept in calculus; the connection between
Motion with constant acceleration
With velocity defined as the derivative of position and acceleration as the derivative of velocity, we can immediately ask
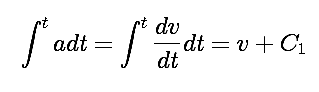
Integration of the constant
Similar reasoning gets the equation for
The work-energy theorem
The work-energy theorem arises naturally from considering the definite integral
The right hand integral can be done to give the difference in kinetic energy. Potential energy arises from consideration of the individual contributions to the force integral. Those which are path independent lead to potential energy differences.
Center of mass
If we define momentum of a system as the vector sum of the momenta of its parts, and the mass of the system as the sum of the masses of its parts, the center of mass arises by requiring that the velocity of the system be equal to two things:
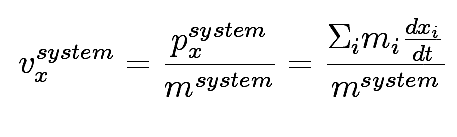
and
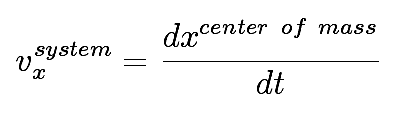
The usual result is obtained by setting the constant of integration equal to zero.
-
Contact Information
Contact Number: 717-871-4297
Email: physics@millersville.edu