Experiment of The Month

In this month's lab we estimate the average diameter of a family of marbles, with the only measuring instrument being an unmarked 1 meter stick. We position about 12 marbles in front of the meter stick. To understand the measurement, first consider a hypothetical measurement.

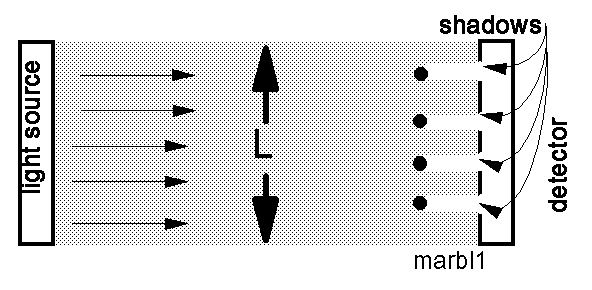
Imagine a long light source, as shown in the figure below, shining parallel rays of light towards the marbles and the meter stick. The shadows cast by the marbles are as wide as the marbles themselves. The total amount of shadow is the sum of the widths of all the marbles. We will call the ratio of the total shadow to the length of the detector by the name "R." This ratio is related to the diameter, D, of the N marbles by

ND = RL

where L is the length of the meter stick, 1 meter.

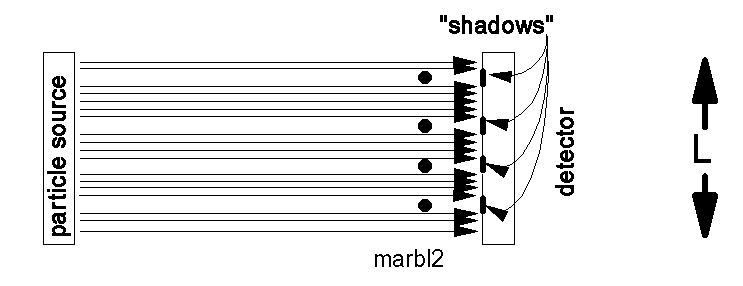
If we replace the light source with an emitter of tiny particles, the result is the same, except that we have a particle detector instead of a light detector, as in the figure below.

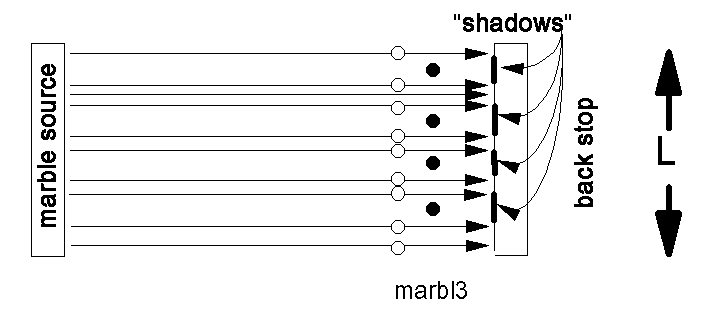
Finally, for the actual experiment, we replace the particles with another marble, which we roll repeatedly at the target marbles. We start the marble at different places, about 1 meter away from the row of target marbles, and roll without aiming. We repeat this M times, and count the number of times that our "shooter" marble hits one of the target marbles. The ratio of number of hits to the total number of rolls is the same as the ratio, R, in the previous experiment.

There is an important difference, however: Because the diameter of the shooter marble is large (the same as the target marbles), the size of the "shadow" of one target marble is twice its diameter, as can be seen in the figure below.

The marble diameter is related to the ratio, R, of hits to total shots by

N(2D) = RL

This can be solved for the diameter, D, which is a centimeter or so. It is remarkable that this measurement does not use any of the subdivisions on the meter stick.

It seem reasonable that the more times you roll the shooter marble, the more accurate will be your average value of the diameter. This idea is tested, using the "standard deviation of the mean" as the estimate of the uncertainty in the diameter. We expect this uncertainty to decrease as the number of rolls increases.

We must first develop the idea of the standard deviation of the mean. We divide the students in the lab into groups. In the example used here, there were 10 groups of 2 students each. Each group will report a value for the marble diameter. The class average (mean) is calculated by averaging these 10 reports, and the standard deviation of the mean is calculated from the same 10 reports.

To obtain a value for the diameter, a student rolled the marble 25 times and counted the number of hits. Each group repeated this 9 times, getting 9 values for D. What follows is a series of reports to the class. With each report, a mean and standard deviation of the mean is calculated.

For the first report, each group simply reports the first result that they obtained. This report has number of trials equal to 1.

For the second report, each group averages their first two results, and reports the average. This report has the number of trials equal to 2.

This continues, until on the blackboard are 9 standard deviations (of the class mean); each for a different number of trials averaged to create a group's reported diameter.

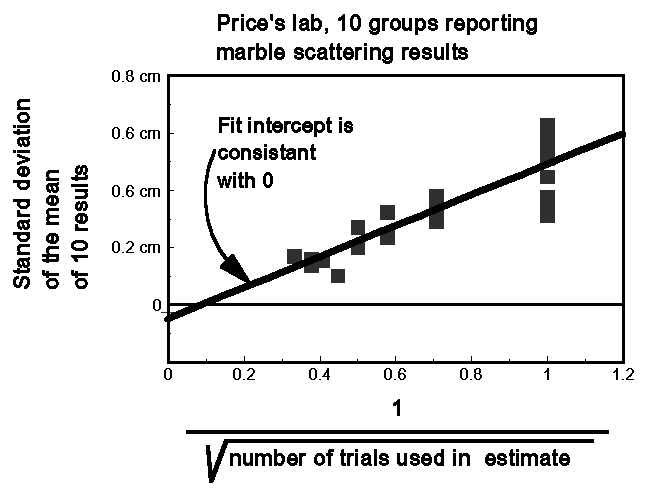
After some discussion of just how to make plot (and some trial and error using Excel spreadsheet plots), the standard deviations are plotted versus 1 over the square root of the number of trials used by the group to create the report. The graph for a lab run by Dr. Price is shown below.

The data certainly show that the uncertainty decreases as the number of trials is increased. The results fit remarkably well to a {1 over the square root of the number of trials} dependence.

The reader will notice more points than expected. When students reported just a single trial, most of the data were unrepresented in the standard deviation. This report was repeated with just the second trial reported, then the third, etc., to produce 9 independent values for the standard deviation of the mean for one trial. A similar scheme was employed for the reports with 2,3,and 4 trials. The virtue of this is to give a rough idea of the scatter of the values of the standard deviation itself.

A least squares fit to a straight line gave an intercept consistent with zero, and a "goodness" measure of R^2=.76.

Back to Main Page of  Marble Scattering Experiment