Experiment of The Month

The MU Physics Department does not claim to have invented these labs. The origin of these labs is currently unknown to us. Our labs do not have written instructions. In keeping with this spirit, the description given here will be brief and general. The intent is that each performance of the lab will be unique; in each nature will reveal a slightly different face to the observer.

There is an ancient rule for a falling ball: The velocity of the ball is constant. We ask if we can measure accurately enough to test this rule.

It has been argued that it is impossible for a dropped ball to instantly acquire a velocity because nothing is instantaneous. However, the common modern model (in which the acceleration of the dropped ball instantly changes from zero to a non-zero constant) suffers under the same criticism.

To test the idea, it is not enough to drop the ball from a single measured height and measure the time of fall. Either a (constant) velocity or a constant acceleration may be calculated from these measurements. This single experiment does not let the experimenter decide which model is correct.

 

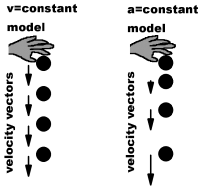
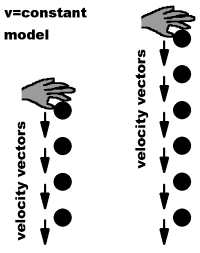
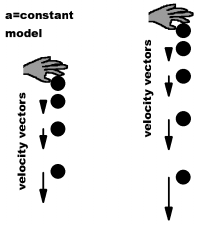
No matter which model is correct, the following is correct: The distance fallen divided by the time of fall is equal to the average velocity. If the velocity is constant, then the average velocity is also the instantaneous velocity. If we drop from a larger height, the two models make two different predictions: If the velocity is constant, we will measure the same average velocity as before. If the velocity is not constant (e.g., if the speed increases as the ball falls) then the average velocity will be different for the new drop height. For example, if the speed increases as the ball falls, the new average velocity will be larger because some larger velocities contribute to the new average.

 

We drop the ball from three heights (1,2, and 3 meters are possible within the lab), and measure the fall time with a stopwatch. Since the error made in time measurement is about the same no matter what the drop height, we could get more accurate results if we used larger distances. We repeat the measurements; each person measures the fall time for each drop height times (e.g. 6). We use excel to calculate the velocities and average velocity for each height. We take the uncertainty in velocity at a given height to be the standard deviation of the velocities for that height.

 

The figure shows a plot of the velocity data for drop heights of 1, 2, and three meters. Each point represents the average velocity determined by a single experimental group. Ten experimental groups thus gives us ten points at each height. The graph shows that, although the 3 meter data overlap the 2 meter data, the 3 meter velocities are distinct from the 1 meter velocities.

 

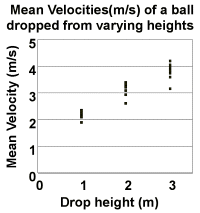
On a good day, our measurements have uncertainties low enough to just show that the average velocity increases in magnitude with increasing drop height. Even on a good day we come away with an appreciation of how hard it was to do this experiment without modern stopwatches. We note that it took technology to move the discussion of how an object falls from unresolved philosophical argument to observed fact.