Experiment of The Month
Statistics of Marble Scattering
The MU Physics Department does not claim to have invented these labs. The origin of these labs is currently unknown to us. Our labs do not have written instructions. In keeping with this spirit, the description given here will be brief and general. The intent is that each performance of the lab will be unique; in each nature will reveal a slightly different face to the observer.
In the marble scattering laboratory, students measured the mean diameter of a population of marbles by scattering "shooter" marbles from target marbles. They used a statistical result for the uncertainty in their answer, which is derived here. The result is that the fractional uncertainty in the answer, for N repeated measurements 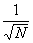
10 other groups do the same thing. To estimate the uncertainty in a single groups
Since the experiment has been repeated by the other groups, we are able to answer this question. We calculate the standard deviation of the mean of the 10 diameters reported by the 10 groups. We call this error estimate the "standard deviation of the mean."
In the lab, it is verified that the standard deviation of the mean, divided by the mean value for the diameter (the "fractional deviation") is equal 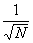
The article is divided into two segments: The current page, which sets up the language and application, and Dr. Miziumski's page which shows the derivation.
We can display the data in an array, as shown, to help understand the analysis.
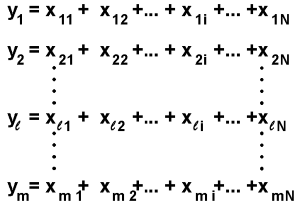
In terms of the marble diameter experiment, each x in the array represents a single calculation of marble diameter, based on (for example) 25 rolls of the shooter marble. N is the number of those measurements (9, for example) that a single group used in their calculation of the mean diameter.
With this value for <y>, we can calculate the deviations,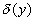 and
and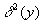 from the mean for each y in the array. The average over
from the mean for each y in the array. The average over 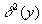
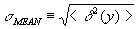
It would be very useful to an individual group if there were a way to calculate the standard deviation of the mean based upon just their own data, without reference to other groups' results. Dr. Miziumski shows that the standard deviation of the mean is related in a simple way to the standard deviation of the x values.
This deviation of x's is calculated from the difference, 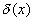 between each individual x value and the average value of the N
between each individual x value and the average value of the N 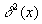
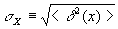
The result is that
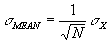
This specific result leads to a much more general result: The fractional deviation of the mean is given by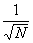 . To see this, we keep the number of target marbles (typically 12) and the number of shots per trial (e.g. 25)
. To see this, we keep the number of target marbles (typically 12) and the number of shots per trial (e.g. 25)
When this happens, the number of hits (out of 25 rolls of a shooter marble) decreases. The calculated result for marble diameter stays the
Take this towards the extreme, so that most rolls of the shooter give no hits, giving a value of 0 for x. Approaching the extreme, the average value for x from any particular set (N trials of, for example, 25 rolls) approaches 0. The only other value that occurs with noticeable frequency is that from one hit for the 25 rolls of the shooter; x=L/25. Since the average value in a set of N trials is much closer to zero than to L/25, the x deviations in a given set are (essentially) the x values in the set.
This means that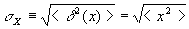 . Thus
. Thus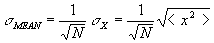
Thus
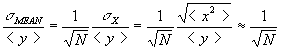
Result
Let x be as "Stochastic" or "Random" variable. This means that x occurs in "random sequences" x1, x2,..., xi,... of numbers with values belonging to a definite range (EG., +1 for heads, -1 for tails in a coin toss) each value appearing with a specific frequency (E.G., half heads, half tails.)
Partition a sequence of x into groups of N terms. Let the sum of the terms in the be yl . The object is to show that for long sequences, the averages (<>) of the squared deviations (d) of x and y are related by
<d2(y)> = N <d2(x)> .
The mean of y is given by 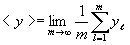 . In a sequence of x, refer to the ith element (i = 1,2,...,N) of the l th group as xl , i . Then the corresponding element of the y sequence is
. In a sequence of x, refer to the ith element (i = 1,2,...,N) of the l th group as xl , i . Then the corresponding element of the y sequence is 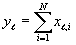 . Notice that the mean of y is related to that of x by the expression
. Notice that the mean of y is related to that of x by the expression
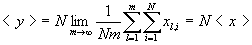
because Nm is the total number of x values.
The deviation of the terms in the y-sequence from their mean can be expressed in terms of the corresponding deviation for x as follows:
so that
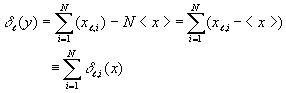
Then the average of the squared deviation of y satisfies the equation
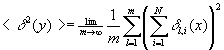
so that
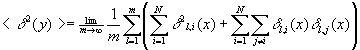
or
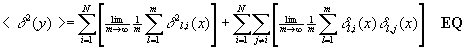
.
Using the definition of independence sequences of random variables, easily justified using plausible arguments*, the value of the second bracketed term above is seen to be zero.
The bracketed expression in the surviving (first) term on the right hand side of EQ. is just <d2(x)> , so that the equation yields the predicted relationship,
* In the sum
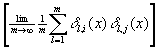
sort the terms so that they are listed in order of increasing value for 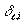 . Since there are a large number of terms, many will be found for which
. Since there are a large number of terms, many will be found for which 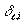 is the same, e.g.
is the same, e.g. 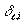 = .21. We collect those terms together. The constant value (e.g.
= .21. We collect those terms together. The constant value (e.g. 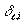 = .21) multiplies the sum of many terms
= .21) multiplies the sum of many terms 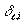 over
over 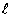 .
.
But the sum of many 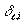 's is zero. Repeating this, we see that the entire bracketed term is zero.
's is zero. Repeating this, we see that the entire bracketed term is zero.
-
Contact Information
Contact Number: 717-871-4297
Email: physics@millersville.edu