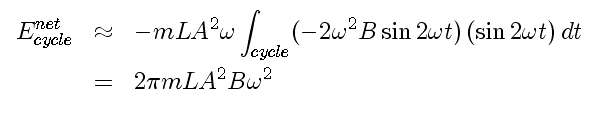Experiment of The Month

The loudspeaker driving mechanism (at the top of the photo at the left) pulls the pendulum pivot up each time it passes through its minimum height. (the pendulum pivot is about 3cm below the brass coupler in the figure. In this part of the motion, the speaker causes no change in the tangential velocity of the bob. The bob simply moves vertically. In the figure, the bob is about 1 meter below the brass coupler.

When the bob is at its greatest height, beginning to swing back down, the loudspeaker lowers the pivot point. The effect of this is to increase the size of the tangential component of the gravitational force on the bob. Because of this, the tangential acceleration is greater than it would have been for a stationary pivot. The net result is larger tangential velocity.

The pumping cycle has increased the tangential velocity and, thus, the maximum kinetic energy of the bob. This increase of energy compensates for energy lost to friction during the course of one cycle.

A more formal analysis is as follows:

The pendulum pivot moves up and down as sketched in the figure below. The equations for vertical and horizontal components of velocity of the mass m (the bob) are also shown

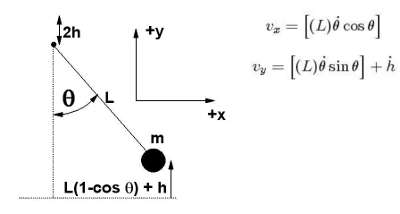
We can calculate the kinetic energy of the system using these velocities:

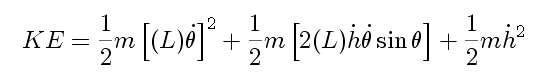
and using the kinetic energy, we can calculate the Lagrangian, L, for the system:

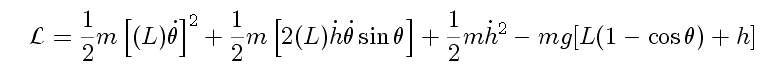
We use the Lagrangian method to calculate the equation of motion for the angular component of motion:

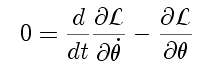
which yields and equation of motion:

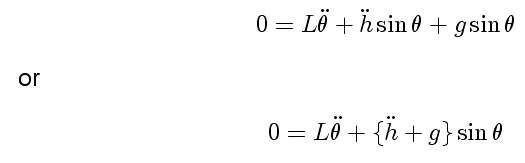
We see that the driver perturbation adds in as a modulation to the gravitational field. If we make h a sinusoidal function of time, and linearize the sine function, the equation of motion is known as Mathieu's equation. (See Landau and Lifshitz Mechanics, page 82.)

We can determine the energy added during one cycle by integrating the power over one cycle:

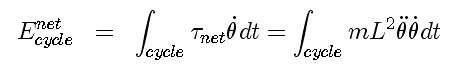
For our system, this is

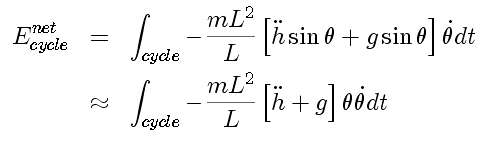
Now we make a lucky guess for the behavior of the angle:

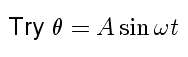
and a lucky guess for the phase of a sinusoidal driver:

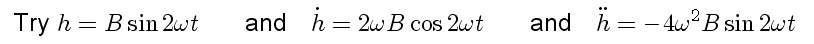
and find for the energy added during a cycle for sinusoidal position

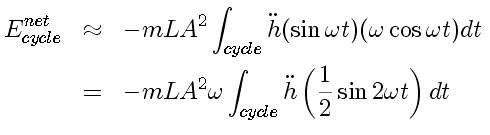
and for the sinusoidal driver, finally