Experiment of The Month

This experiment of Dr. Miziumski's was most recently done in Physics 103, our course for non-science majors. The purpose is to measure the area of one of the tiles on the floor. The method is to throw bits of paper at the floor and count how many times the bit of paper lands on a corner between floor tiles. Students find it a pleasant surprise when it works. They are more surprised by the fact that there is no limit on the accuracy of this measurement: The more bits you throw, the more accurate the measurement becomes.

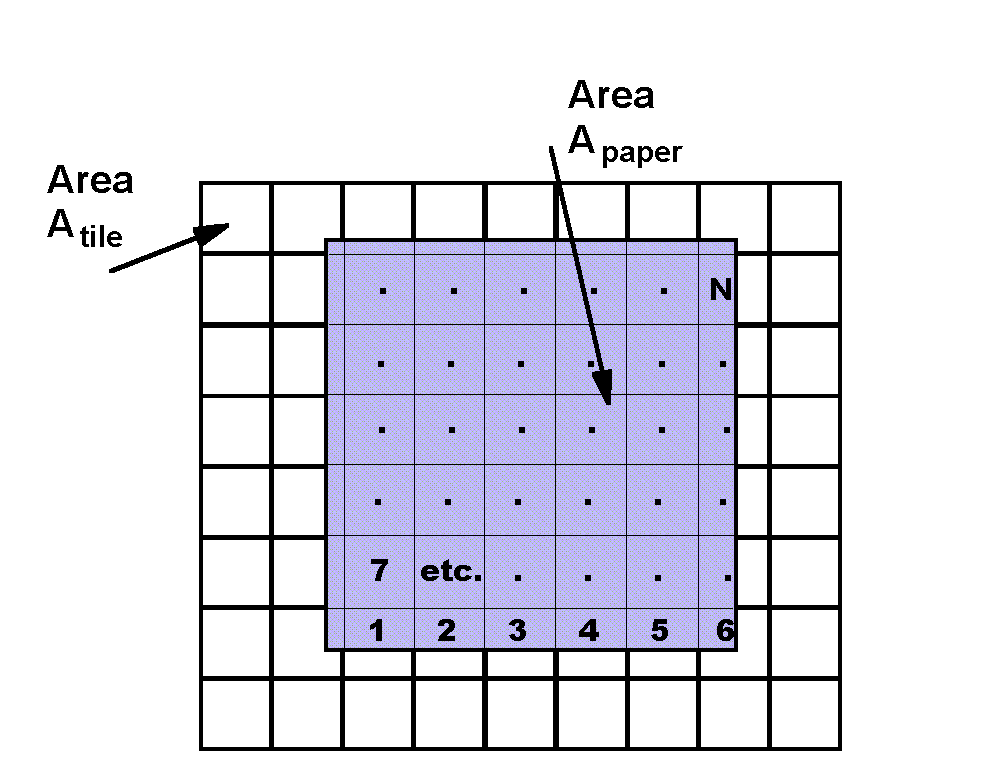
The figure at the right shows a section of the floor, with many tiles. Lying on top of the tiles is a large sheet of paper. The paper is not completely opaque, so that the edges of the floor tiles can be seen faintly through the paper. (You may have to view the image full sized in order to see all of the faint lines.)

If we know the area of the large sheet of paper, A_paper, we can estimate the area of the floor tile by counting how many tiles the paper covers, N. Then

A_tile = (A_paper)/N

The counting is indicated by a number at the center of each faint floor tile, replaced by dots when we get tired, all the way up to N.

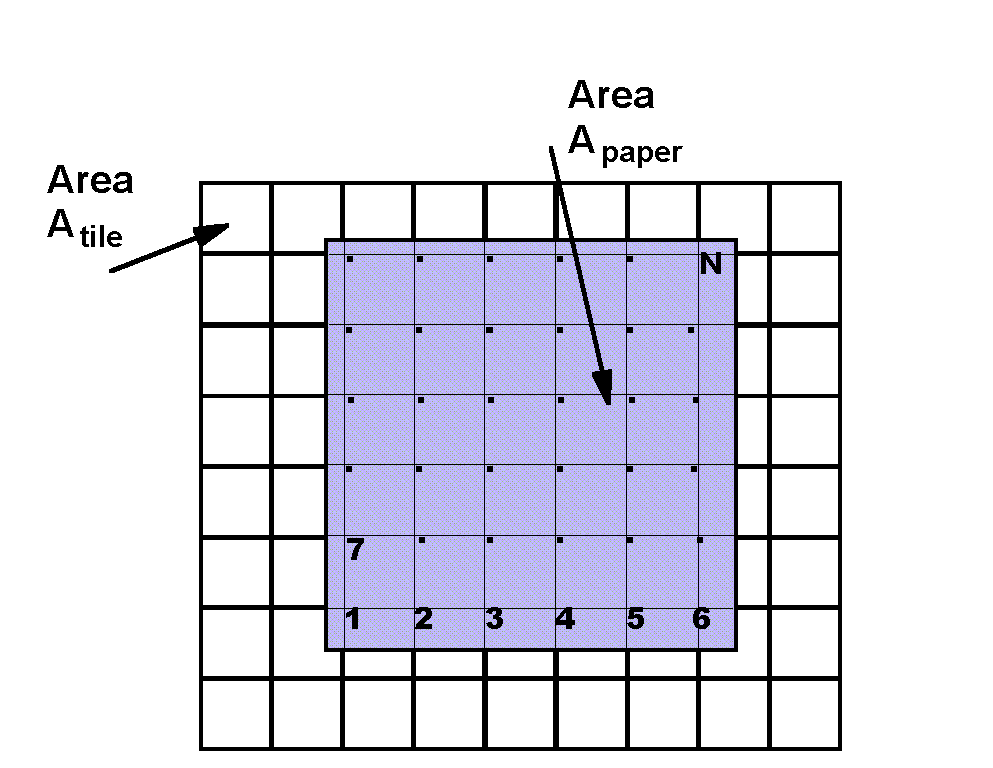
It turns out to help in thinking of this problem if we move the dots from the center of the square to the upper left corner of the square, as in the figure at the right. The count remains the same. It is easier to visualize this way, allowing one corner to represent 1 square in the count.

Still,

A_tile = (A_paper)/N

but all we have to do is count the number of corners that were covered.

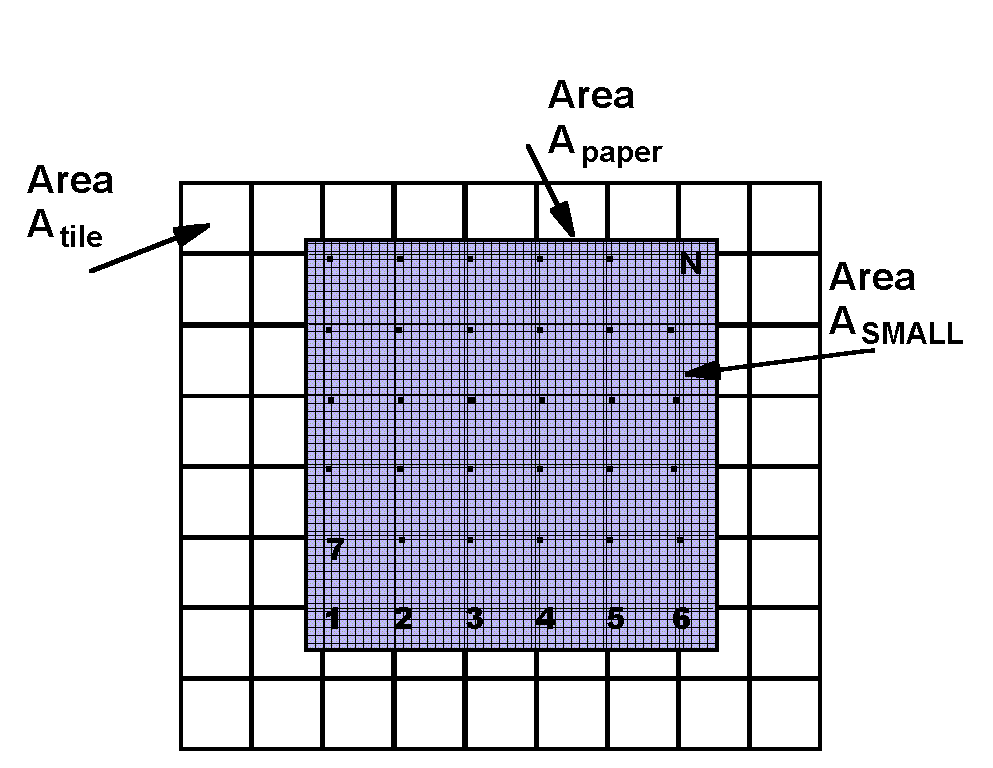
Finally, we imagine that we cut the large paper into many small squares.

Let M be the number of small bits of paper, so that if A_small is the area of a small bit, then

A_paper = MA_small

If we tape them together to reassemble the large sheet, we still can count corners covered and calculate

A_tile = (A_paper)/N = ( MA_small)/N.

We could also put the bits of paper down one at a time, and count the times when one of the bits is placed on a corner. Now we see that N is just the number of bits that happen to land on a corner.

Of course the order in which we put the bits down does not matter, nor does the identity of each bit of paper. In fact we could use the same bit of paper M times, picking it up and putting it back down, and we would get the same answer for the area.

The remarkable statistical result is that we can throw a bit of paper randomly at the floor, M times; count the number of times, N, that it lands on a corner, and we will still get the right answer for the area.

A_tile = ( MA_small)/N.

Throwing the bit of paper more times is equivalent to dividing the large area more finely (or to using a larger sheet of original paper). In either case, the effect of throwing the paper more times is to increase the accuracy of the estimate.

In lab, each student throws a piece of paper 100 times. The size of the paper is selected so that a corner is covered about half the time, just to keep things interesting. (If the paper covers two corners on one drop, N is increased by 2, not 1.) In a class of 20 students, this gives M of 1000, and a reasonably accurate measurement of the area of the floor tile.

Dr. Miziumski's experiment is actually an inverse of this description: his students know the area of the floor tile and use the equation above to calculate the area of an unknown sheet of paper. In this way the area of a sheet with complicated shape is easily found. Also, if the sheet of paper is a circle, this experiment can be used to determine a value for p.