Experiment of The Month
Circular Pattern in Collisions of Identical Balls
 James Stoltzfus needed to make up a laboratory that he had missed. The experiment was to determine if energy and momentum were conserved in a collision between two identical steel balls. Rather than repeat the experiment that had already been done, he did an experiment which extended the previous results.
James Stoltzfus needed to make up a laboratory that he had missed. The experiment was to determine if energy and momentum were conserved in a collision between two identical steel balls. Rather than repeat the experiment that had already been done, he did an experiment which extended the previous results.
The balls were the size of small marbles. One balanced on a tee, while the other rolled down a ramp, flew off the end, and collided with the teed ball. The picture shows the "shooter" ball about to leave the ramp and strike the "target" ball. After the collision, the balls fly away from the collision point and fall to the floor. In the
The collision point is represented by a dot on the floor directly under the tee. This dot is marked by placing carbon paper, facing down, on top of a large piece of newsprint, at the points where the two balls are expected to land.
The balls always take the same amount of time to reach the floor, so the displacement of the landing point from the collision point is a measure of the horizontal component of velocity of the ball. We neglect wind resistance, and the velocities during the collision are all horizontal. As a result, the displacement (collision point to landing point) is proportional to the velocity (and momentum) just after the collision.
For reference, the shooter ball is also rolled with no target ball present. Its landing point is a measure of the momentum of the system just before the collision. A ball dropped directly from the tee can mark the point below the tee.
Mr. Stoltzfus varied the angle of collision by moving the tee sideways so that the collision varied from nearly head-on to just "kissing." With a
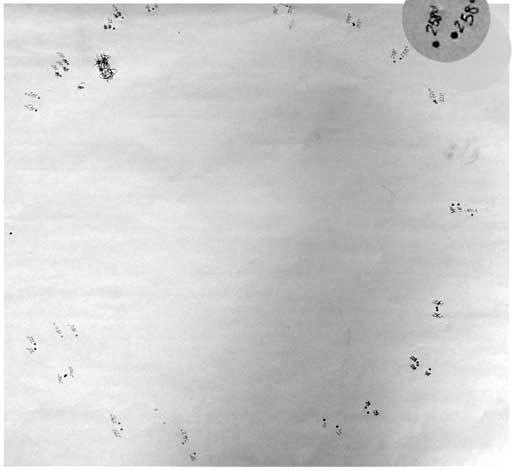

In the photo on the left above, one of the data points (for tee angle of 258 degrees) has been copied, magnified, and inserted next to the actual data points. The numbers refer to the angle that Mr. Stoltzfus read on the protractor. The photo on the right above has had shaded circles added to all the landing points, to clearly identify them. The non-colliding dots are the farthest right in the photos, and the collision point is the furthest left.

The intriguing circular pattern has another feature: Each collision produces a pair of dots; one from each ball. If each pair is joined to its mate by a line, a pattern results which is shown at the right.
The lines form diameters of the circle, crossing at its center. It turns out that such a pattern is predicted for the special case in which momentum and energy are both conserved in the collision. The analysis was sketched by Dr. Nolan, who is teaching physics 231
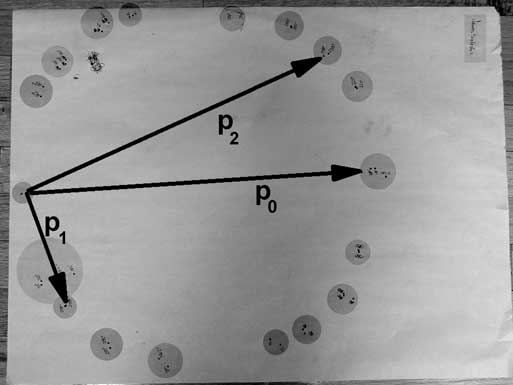
To understand the analysis, we consider the vector displacements of a pair of landing points, from the collision point. We will represent these displacements by the letter "p" to emphasize that they serve as a measure of the momentums after
Similarly, the displacement from the collision point to the landing point of the uncollided "shooter" ball is represented by "p0" because it serves as a measure of the momentum of the system before the collision. An example from the collision
The vector analysis of the problem indicates two salient points. First, the momentums of the two balls are perpendicular to each other. In the notation of the picture, p1 is perpendicular to p2. Second, the circle has a radius equal to half of p0.
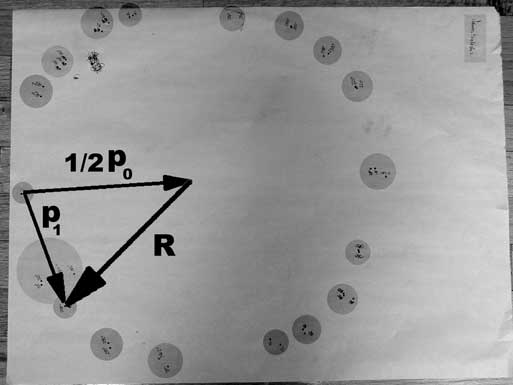
To begin the analysis, we consider two vectors, p1 and half of p0 as shown in the figure at the right. Each point appears to fall on a circle of radius, R. R is evidently also of the same magnitude as half of p0. There is also a vector R, from the center of the circle to a particular landing point, p1. The vector relation shown is written algebraically as
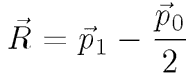
provided that the points really do fall on a circle.
Our algebraic aim is to show that the magnitude of R is 1/2 p0 for every landing point in the data. It turns out that this will be true if both energy and momentum are conserved during the collision.
Conservation of momentum tells us that
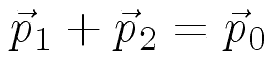 .
.
If we neglect any vertical motion during the collision, then energy conservation tells us that
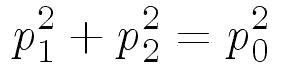 .
.
We combine these two by replacing p0 with the vector sum of p1 and p2, and calculating the square of that new vector:
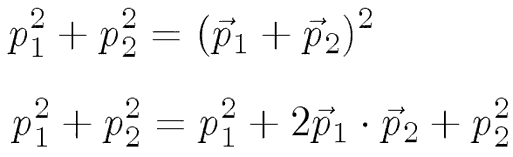 .
.
This can be true only if
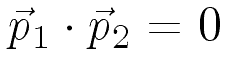 ;
;
that is if the two scattered momentums are perpendicular to each other. Returning to our calculation for the magnitude of the radius, we have
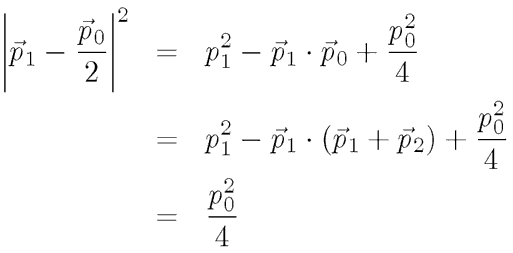 .
.
That is,
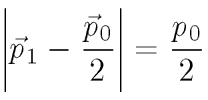 .
.
That is, for any landing point p1, the distance to the point 1/2 p0 is always the same. The pattern is a circle provided that energy and momentum are conserved.