Experiment of The Month
The Helmholtz Resonance
Dr. Miziumski lead our students in musical acoustics (a required course for music majors) through this investigation of the Helmholtz resonator, a fancy name for the "jug" in jug-band music. A detailed discussion can be found here, but the basic ideas are not hard to come by.
In the photograph, Dr. Miziumski blows over the top of a round flask to produce the tone that you can download here . One of the pleasures of playing the "jug" is that such a small device produces such a low pitched tone. To get such a tone (about 200Hz) from the resonance tube described at the end of an earlier article, the length of the tube would have to be about 50 cm, instead of the 15cm in the photo.
Using only audible sound and no electronic data collection, we can use the "tap tone" of the jug instead of the "whistle" tone from blowing into it. To get the tap tone, just tap the fingers on the top of the jug. The jug responds with the same tone as before, dying away like a struck bell, but not ringing as long as a bell.
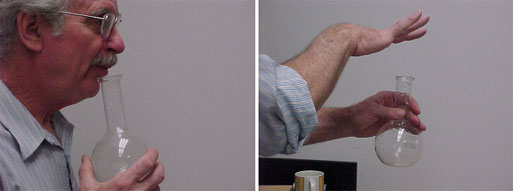
Could this resonance be a standing wave? If it is a standing wave, with the container being open at one end and closed at the other, then the fundamental tone has a wavelength equal to 4 times the length of the tube. If this is the case, then the frequency should go up if the length of the column (and the wavelength) get shorter. That can be tested by putting some water into the jug, as shown on the left below.

When the water is added, the frequency (pitch) of the tap tone goes up. So far, so good. Now Dr. Miziumski tips the jug as shown on the right. The air column is back to its original length. If this is a standing wave resonance, the tap tone pitch should go back down. It does not.
The pitch of the jug is independent of the length of the air column. We are forced to conclude that some other mechanism is responsible for selecting the pitch of the jug.
A model that works surprisingly well is this. We think of the gas in the neck of the jug as a separate entity. When tapped, the neck air is pushed down into the spherical part of the jug. Pushing down into the spherical region raises the pressure there.
It is plausible (and reasonably true) that a 10% compression (decrease in volume) of the spherical air causes a 10% rise in the pressure there. Now, the change in spherical volume is proportional to how far down the neck air moves, and the force upward on that neck air is proportional to the increase in pressure (above atmospheric pressure).
But the musical acoustic students know that when a mass experiences a force proportional to the displacement, the result is simple harmonic motion, like a mass on the end of a spring. The natural frequency is determined by the spring stiffness and the mass that is moving.
Here, the mass that is moving is the mass of air in the neck, and the stiffness is determined by the air in the spherical part of the jug. When the volume of the spherical part is reduced, the air there is "stiffer" and the natural frequency is increased, no matter what the length of the air column. Some details follow:
Let the cross sectional area of the neck be called A, and the volume of the spherical part be called V. When the plug of air in the neck pushes down a distance x into the sphere, V changes by xA, and the pressure increases by the same fraction.
(pressure increase) = P (xA/V)
The net force back on the plug of air is this pressure increase multiplied by the are of the neck:
Fnet = A(pressure increase) =[(PA2)/V]x
This looks like a spring restoring force because the force on a mass by a spring is given by
Fspring = (-) kx
where k is called the spring constant, and the minus sign indicates that the forces always pushes the mass back towards equilibrium at x=0.
If we know the mass of the air plug, we can treat it like a mass on a spring and get the simple harmonic motion of that mass. The mass of the air plug is
m = (density)(plug volume) = (density)(AL)
where L is the length of the neck.
We can use [(PA2)/V] for the spring constant and the formula for the frequency (f) of a mass on a spring:
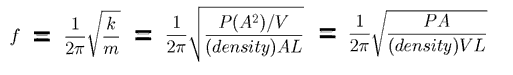
The flask in the pictures has a volume of 500mL, neck length about 8cm, neck inner diameter about 3cm. Using 1 kg/cubic meter for the density of air, and 105 Newtons/square meter for air pressure, we find a value for the predicted frequency that agrees fairly well with the observed frequency.
A second test of the formula can be made with a soda bottle, as shown below.

The pitch of the bottle on the left is about 0.180 kHz. On the right, the length of the neck has been (roughly) doubled by adding a segment of neck from another bottle. The pitch of the bottle on the right is about 0.150 kHz. The formula predicts that the frequency is proportional to the square root of the neck length, so the pitch should go down by a factor (square root of 2) when the length is doubled.
That is, the pitch should change by about 40%. In fact it only changes by about 20%. (Music majors agree that it changes by a minor third; also a 20% change.) The soda bottle does not fit the Helmholtz model as well as the round bottom flask. The standing wave model predicts only a 10% change, leaving the soda bottle between the two models.
The difference between a Helmholtz resonator and a tube is in the ratio of neck area to body area. For the tube the ratio is 1:1, and to get a good Helmholtz resonator, the ratio should greater than 10:1.
-
Contact Information
Contact Number: 717-871-4297
Email: physics@millersville.edu