Experiment of The Month

Our Dr. Cooney noticed the pattern shown the left displayed on the wall behind his desk. It was caused by sunlight passing through the holes in venetian blind slats. (The holes allow the support strings to pass through the slats.) Shown above is a larger view. The light beam from the sun enters the left edge of the Lucite shelf in the middle of the monitor support. Internal reflections keep the light beam within the thickness of the shelf. The light travels the length of the shelf as it would in a light pipe. It exits on the left, finally hitting the wall.

The figure below shows a shortened version of the geometry.

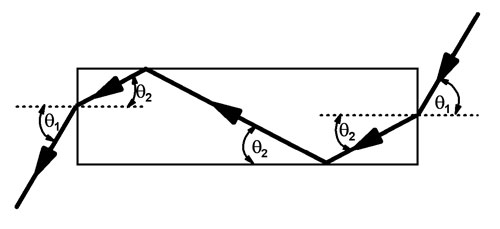
Light enters the plastic from the air with angle q1 and Snell's law tells us how to calculate q₂ .
n sin q₂ = sin q₁
where n is the index of refraction of the plastic.

If the angle q₂ is small enough, the light will be totally reflected at the bottom side of the plastic. This total reflection is repeated at the top, and so on until the light exits at the left end. The exit angle is the same as the entrance angle.

(It is an interesting exercise to show the following: If the wall is vertical and the bottom is horizontal, and if n is greater than the square root of 2, then any light that enters will be totally reflected in this way, no matter what the incoming angle.)

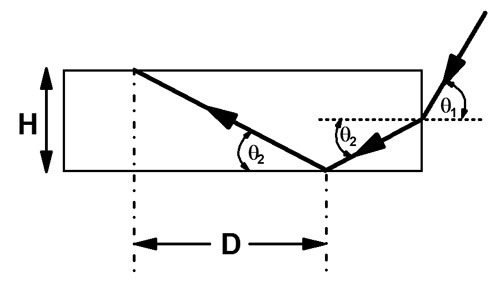
There is a characteristic "skip distance," D, for this light path: the horizontal distance that the light travels while moving from top to bottom of the plastic. Using the notation in the figure,
D = H/(tan q₂ ) .

Dr. Cooney's shelf is .5cm thick and 50 cm long. The index of refraction of the plastic can be taken as 1.5 and the entrance angle is about 45 degrees. Then D is about 0.9cm. In a 50 cm slab of plastic, the light will make about 53 skips before it exits.

If the index of refraction changes slightly, q₂ will change and the number of skips can change. To change by one skip, the length D needs to change by about .9/50 cm, or about .02 cm. We can use differentials to estimate the change in index of refraction that would make this happen:

dD = H d(1/(tan q₂ ) = Hdn/(-n sinq₂ sinq₁ )

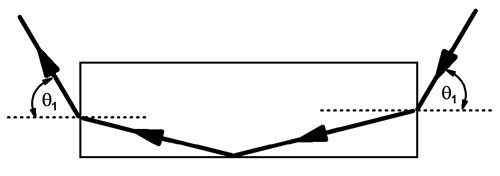
For our example, a change in n of about 0.02 would cause a change of one skip for the trip from one end of the shelf to the other. If we increase n by about 0.01, the light would leave the end traveling up instead of down. A simple example of the effect of increasing n ( changing from 2 reflections to 1 instead of 53 to 52) is sketched below.

From data quoted in Hyperphysics from Serway & Jewett, this is about the difference in index of refraction for acrylic from the upper (blue-green) half of the spectrum to the lower (orange red) half of the spectrum. It seems that this dispersion effect accounts for the fact that the upper light beam is mostly red, and the lower beam is mostly blue.

Dr. Cooney took another picture a few minutes later, after the sun's motion had changed q1 slightly. In this picture that change of angle put the blue on top and the red on the bottom.