Experiment of The Month
Dissection of a Statics Demonstration
The MU Physics Department does not claim to have invented these labs. The origin of these labs is currently unknown to us. Our labs do not have written instructions. In keeping with this spirit, the description given here will be brief and general. The intent is that each performance of the lab will be unique; in each nature will reveal a slightly different face to the observer.
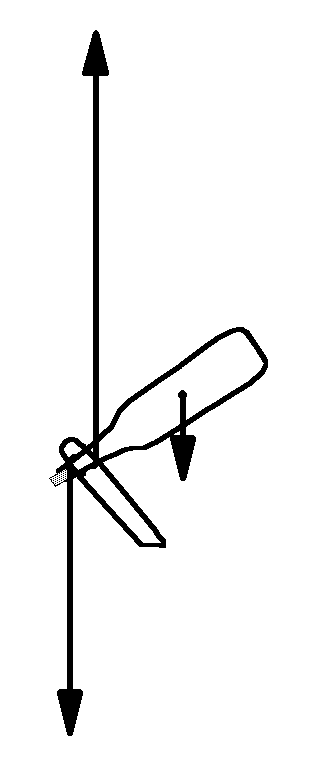
The figure shows a statics demonstration, in which a wine bottle is balanced at a surprising angle. The bottle may be full or empty. In the figures here, it is empty. We will examine the torques and forces for several views of the system.
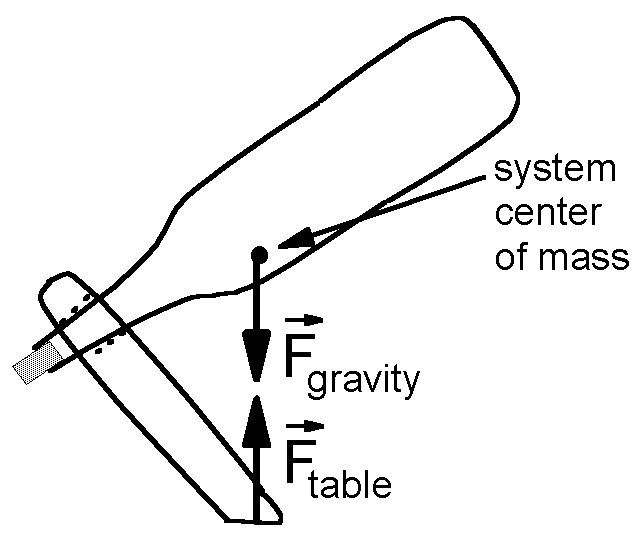
The simplest view of the system ignores its internal structure and says simply that the force of gravity acting on the system plus the force by the table on which it sits must add to zero. This view assumes that the center of mass is directly above point at which the system touches the table.
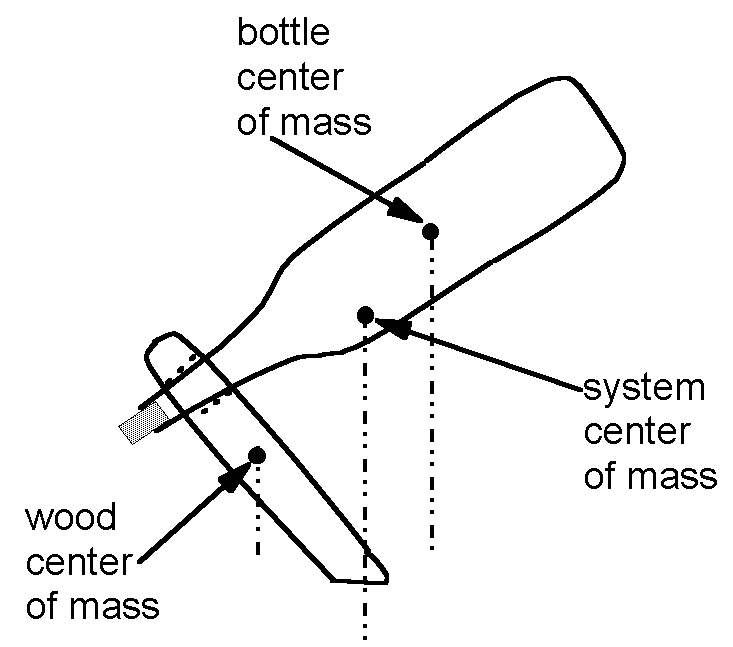
Looking in slightly more detail, the center of mass of the system can be determined from the location of the center of mass of the wood support and the center of mass of the glass bottle. These two views are sketched below:
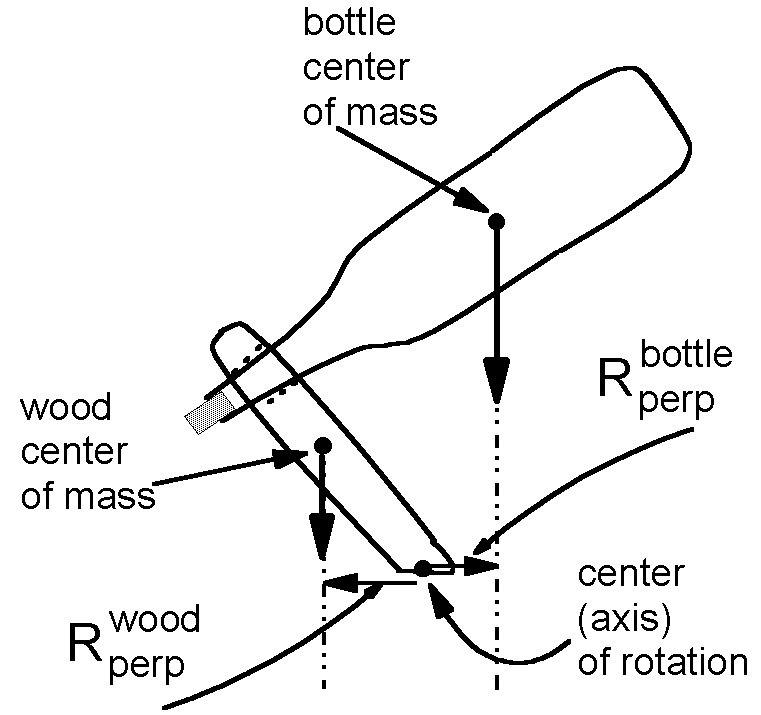
The next more detailed view still requires that the total force on the system be zero. It also considers the torques associated with the force of gravity on the two centers of mass: that of the wood and that of the bottle.
The figure at the right shows those two forces, and the moment arm associated with them. The bottom of the wooden support has been chosen as the center (axis) of rotation so that the torque due the force by the table on the support is zero (because its moment arm is zero).
Since the bottle has larger mass than the wood, the gravity force vector drawn for the bottle is longer than the gravity force vector for the wood. The fact that the moment arm (called Rperp in the figure) is smaller for the bottle than for the wood is essential: The product of moment arm with force is the torque, and the two torques must have the same magnitude (opposite direction) in this simple problem.
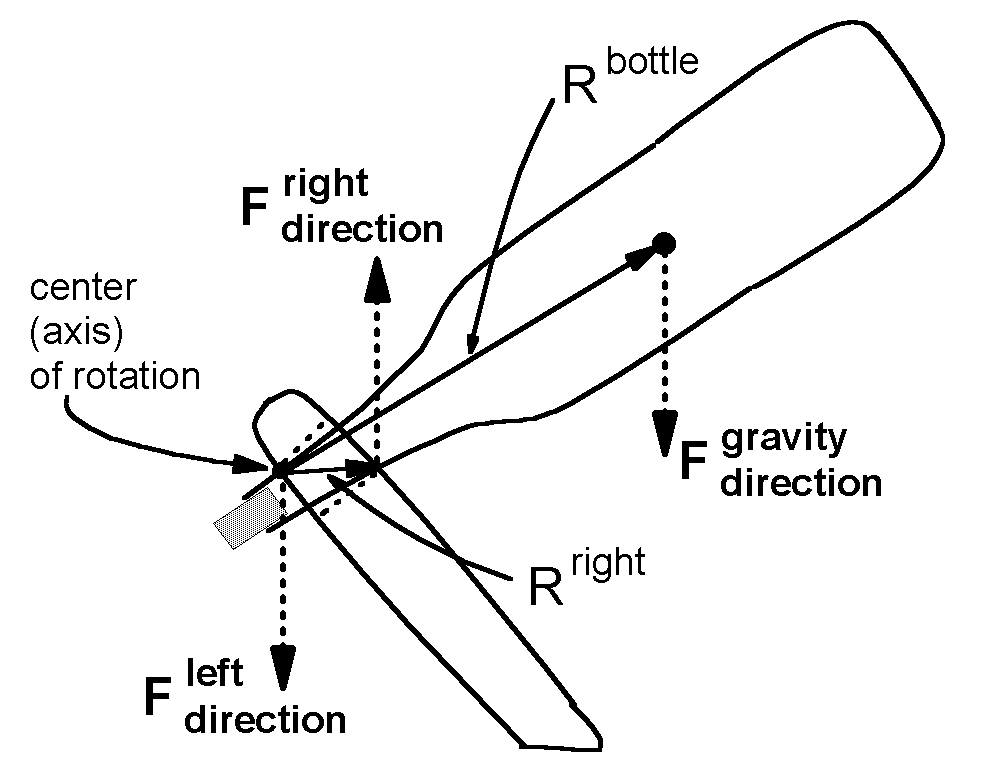
Finally we consider the equilibrium of the bottle alone. To do this, we must recognize that the wood support has a non-zero thickness. This is necessary to provide the forces which create rotational equilibrium.
The wood touches the bottle at the left end of the hole and the right end of the hole. (The hole is indicated by dotted lines.) The center of rotation is chosen to be at the point where the right edge of the wood touches the bottle.
The force directions only are shown in this figure, for the force at the right edge of the wood, at the left edge of the wood, and by gravity at the center of mass of the bottle.
In this figure, the vector R from the center of rotation to the point of application of the force is shown, rather than the moment arm. The torque due to the force on the left edge is zero because it is applied at the chosen center of rotation.
The force from the right edge must be (about three times) greater than the force of gravity on the bottle, since the moment arm for the bottle is much larger. The downward force by the left edge of the wood must be similarly large to make the total vertical force add to zero. A sketch closer to scale is shown below of the size of the forces.