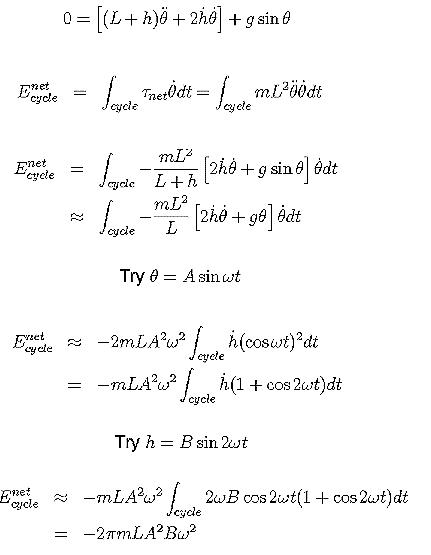Experiment of The Month
A piston-driven pendulum
Several students have made driven pendulums for their senior seminar projects, but it was only recently that the technology allowed a satisfactory result. The problem had been the high "Q" of the pendulums. It typically takes more than 100 cycles for a simple pendulum to lose half its amplitude. This means (roughly) that the driving mechanism must match the natural frequency to a fraction of 1%.
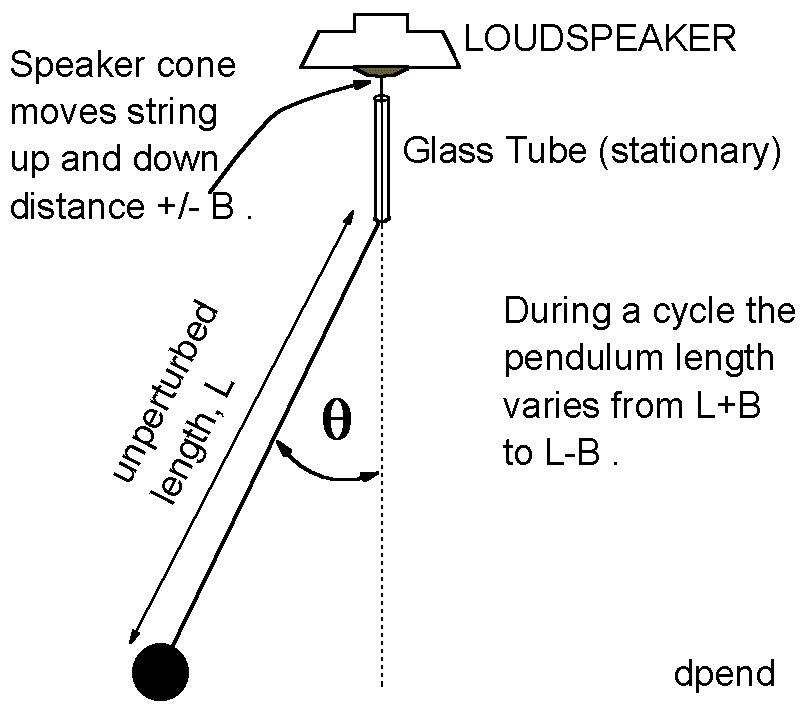
We recently upgraded our introductory laboratory equipment to include Pasco 9587 signal generator/amplifiers. These oscillators can produce a stable 1 Hz signal with a precision of .001 Hz. With these oscillators Senior Meron Wollie studied a driven pendulum. The set up is shown in the figure.
The string for the pendulum was flexible nylon thread. The glass tube has a bore of about 1mm diameter and was about 10 cm long. The pendulum length was about 1 meter, and the mass of the bob was about 100 gm. The angle, theta, shown in the figure was taken to be negative. (Counterclockwise was considered positive.)
The loudspeaker is driven by the signal generator with a frequency equal to twice the natural frequency of the pendulum. When the driver is successfully pumping energy into the pendulum, it pulls up every time that the pendulum angle passes through zero, shortening the length L. When the pendulum is at its maximum angle, the length of the pendulum is increasing most rapidly.
This parametric driving mode is the same as the method of "pumping" a playground swing. The swinger stands up as the swing passes through its low point, effectively shortening the length of the swing.
The pendulum loses energy to wind resistance, friction between the tube and the string, and internal friction within the bending string. When the driver is pumping energy in, the amplitude of the pendulum increases, along with the frictional losses. When the energy input matches the frictional loses, the amplitude stops increasing and the pendulum achieves a steady state.
This driving mechanism depends on the motion of the pendulum. If the pendulum is hanging straight down, and is stationary, then turning on the driver will only cause it to go up and down along a vertical path. The pendulum must be "started" by swinging it by hand before the driver can transfer energy into it.
Roughly speaking, the driver increases the potential energy of the bob by pulling it up as it passes through zero angle. Then the driver allows the force of gravity to convert some of that extra energy to kinetic energy, by allowing the bob to fall an extra distance at large angles. Note that at large angles, the tangential component of the force of gravity is at its largest, so at large angles the force of gravity can cause the largest tangential acceleration.
Ms. Wollie studied the motion of the pendulum experimentally, with special attention to the relative phase of the driver and the bob. She also calculated the power added to the pendulum and found that it is indeed maximum when the driver frequency is twice the natural frequency, provided that the phase relation is correctly set. Her calculations began with using the LaGrangian method of finding the equation of motion for the pendulum of length L+h.
The top equation in the figure at the right is the differential equation for the motion. She used the standard expression for power in rotational systems and integrated over one complete cycle to find the total energy input per cycle. To make a concrete calculate, she assumed a sinusoidal form for the pendulum angle, and a similar form for the driver.
In her paper, Ms. Wollie did not assume that the driver frequency was twice the natural frequency, as was assumed for this figure. Instead, she allowed the driver frequency to be a variable, and obtained an expression for the energy input per cycle, as a function of the frequency. She found that the energy input is indeed a maximum when the driver frequency is twice the natural frequency of the pendulum.
Ms. Wollie is currently studying mechanical engineering at the Georgia Institute of Technology.