Experiment of The Month
The Prettiest Fringes


Frank Crawford, in his classic book titled simply "Waves" calls the interference fringes that can be created with white light "the prettiest fringes." Our Dr. Miziumski showed us how to created these fringes in the Michelson interferometer. They are discussed on the HyperPhysics web site.
Our juniors in intermediate laboratory measured the wavelength of sodium light by varying D (in the figure below), and the separation of the two sodium doublet "D" lines by observing a periodic "washout" of the contrast in the interference fringe rings (more below), and the coherence length by observing the final "washout" of fringes.
In the last lab of the semester they also observed the "prettiest fringes," shown above. (Photo by Paul Folmer.) These fringes used white light from an incandescent (40 watt) lamp.
To understand these, we need some details about the interferometer.
The Michelson interferometer and the reflected images involved are sketched below in some detail.
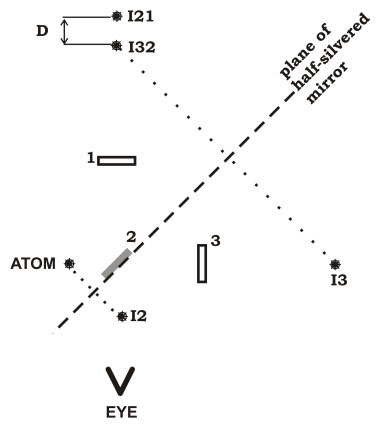
The mirrors labeled 1 and 3 are fully silvered. The mirror labeled 2 is "half-silvered," reflecting half of the light that strikes it. The atom radiates light which strikes mirror 2 first, and half of the light is reflected. The light reflected by mirror 2 forms the image I2, following the usual rules for plane mirrors. (The eye does not see this image because the light which forms it is traveling up toward mirror 1).
The light which travels from mirror 2 to mirror 1 reflects towards the eye. Mirror 1 treats image I2 as an object and forms an image called I21. The eye sees I21 as a virtual object.
The other half of the light from the atom passes through mirror 2 and strikes mirror 3, forming image I3. The light reflected by mirror 3 returns to mirror 2 and half of it (the half that we care about) reflects finally to the eye. Following the usual rules for mirrors, the image I3 is treated as an object and its reflection in mirror 2 is shown as I32.
The eye now sees two virtual sources, I21 and I32. The value of this construction is that I23 and I21 have a definite phase relation. (If the distance D =0 then the two are in phase.) The light from the two images interferes coherently. Imagine that the two virtual sources interfere constructively for a particular value of D. If D is increased then the interference will change, becoming destructive and finally constructive again when the change in D is one wavelength.
In practice, mirror 3 is tilted around two axes until I32 is along the line of sight from the eye to I21. Mirror 1 is moved (vertically in the drawing) to control the distance D.
The image below helps to understand the characteristic "cheating bulls-eye" pattern of the Michelson interferometer.
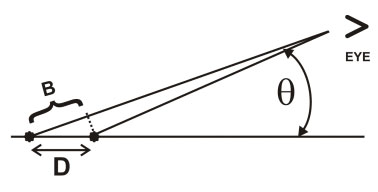
The eye detects bright when 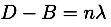 which translates to
which translates to 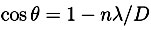 . Expanding the cosine for small angles leads to
. Expanding the cosine for small angles leads to 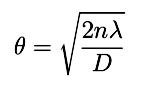 meaning that the fringe rings pack together at larger n.
meaning that the fringe rings pack together at larger n.
To get the prettiest fringes, we make D=0 (by moving mirror 1 for maximum central spot size) and separate the two virtual sources "sideways," perpendicular to the line of sight (by tilting mirror 3 about a vertical axis):
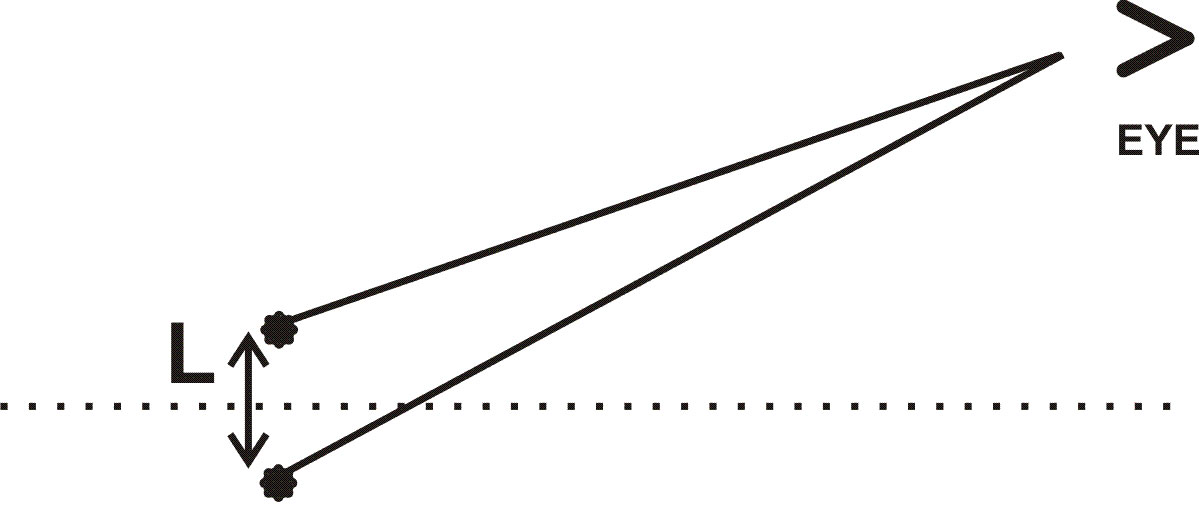
If the eye is placed on the dotted line, it sees bright, for all wavelengths. That is on the dotted line, the light from a light bulb is white. Shifting off, the brights are located following the usual "two slit" rules. The n=1 blue will show first, and the n=1 red will show last as the eye moves away from the dotted line. Because the red wavelength is almost twice the blue, the pattern quickly takes on a rainbow appearance, and soon the overlapping orders return the light to white.
It practice, to find these fringes, use a sodium lamp and make D nearly (but not quite) zero, by making the central "bulls eye" spot large. Tilt mirror 3 so that you see the outer rings as nearly vertical lines, instead of seeing the central "bulls eye." Now replace the sodium lamp with a white incandescent lamp and move mirror 1 slowly in the direction that makes D smaller. Watch for the bundle of black/white/rainbow fringes.
It may be noted that the central fringe above appears to be black instead of white. This indicates that the two sources are 180 degrees out of phase. The best guess for the cause is that one reflection at the half-silvered mirror is from air to glass, and the other is from glass to air. The first has a 180 degree phase shift upon reflection and the second does not.