Experiment of The Month
Filter drop and statistics
The MU Physics Department does not claim that we invented these labs. Actually, the origin of these labs
We use this lab to introduce the ideas of average and standard deviation. It can be extended to study the question of how things fall. (Do falling objects move with constant velocity? constant acceleration? some other way?)
The falling objects
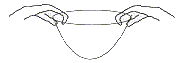
Students work with partners. One student drops a filter from about 2 meters above the floor. A second student starts a
Each individual time is put on the
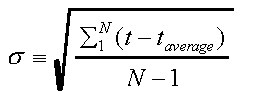
Pairs (or larger groups) combine their data and
- plot a histogram
- calculate the average and standard deviation
- mark the average on the histogram
- mark the interval
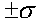 on the histogram
on the histogram - test the prediction that about 2/3 of the times will fall within one standard deviation of the average.
- mark the interval
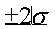 on the histogram
on the histogram - test the prediction that about 95% of the times fall within 2 standard deviations of the average.