Experiment of The Month
Running in the Rain
The MU Physics Department does not claim to have invented these labs. The origin of these labs is currently unknown to us. Our labs do not have written instructions. In keeping with this spirit, the description given here will be brief and general. The intent is that each performance of the lab will be unique; in each nature will reveal a slightly different face to the observer.
Does it help to run in the rain, or does running just change which parts get wet? The short answer is that running helps. The long answer was the subject of a thought experiment for the physics freshman honors seminar, one rainy day in a building too far from the Roddy Science Center.
We supposed several things about our rainstorm: It lasted a long time. It had the same number of raindrops per cubic meter, everywhere. The velocity of the drops was the same everywhere. This way, we can estimate how wet a person gets in a time interval by calculating the "volume of rainstorm" that struck him in that time interval.
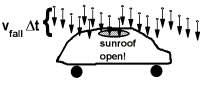
The most simple case is when the target of the rainstorm is standing still, and the rain is falling straight down, as is the case for the open sun-roof of the car in the figure. During a time interval 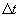 the last raindrop to enter the roof started out a distance
the last raindrop to enter the roof started out a distance  above the car. The volume of rainstorm that falls in the sunroof during
above the car. The volume of rainstorm that falls in the sunroof during 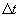 is
is 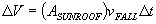 where
where 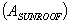 is the area of the opening made by the sunroof. As long as the rain is steady and uniform, the same amount falls in the sunroof, whether the car is moving or standing still. Moving the car only changes which drops fall in - not how many.
is the area of the opening made by the sunroof. As long as the rain is steady and uniform, the same amount falls in the sunroof, whether the car is moving or standing still. Moving the car only changes which drops fall in - not how many.
If we model a person as a box, with a flat top of area 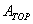 and front (and back) surfaces of area
and front (and back) surfaces of area 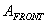 we can make an estimate of how the person gets wet in the rain. We suppose that the person is running in the +x direction, while the rain still falls straight down. The top wetting (during time
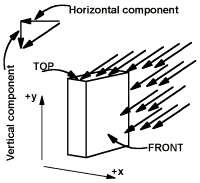
we can make an estimate of how the person gets wet in the rain. We suppose that the person is running in the +x direction, while the rain still falls straight down. The top wetting (during time 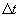 ) is the same as for the car. The front now gets wet because, relative to the box, the rain has a velocity which carries drops onto the front. The figure shows the point of view of the box, with the vertical component of rain velocity the same, but a new added horizontal component in the -x direction.
) is the same as for the car. The front now gets wet because, relative to the box, the rain has a velocity which carries drops onto the front. The figure shows the point of view of the box, with the vertical component of rain velocity the same, but a new added horizontal component in the -x direction.
The volume accumulated by the box in time 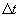 is now
is now
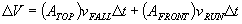
If wind is blowing rain in the +x direction with a velocity 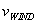 , and we assume for simplicity that
, and we assume for simplicity that 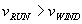 then the result is
then the result is
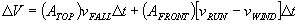
Now the time of interest is the time to run from one building to another, a distance, L, at speed 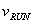 is calculated, and plugged in to find
is calculated, and plugged in to find
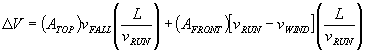
Remarkably this indicates that if there is no wind, the amount of water collected on the front is the same, no matter what the speed - fast or slow. Wind or not, the volume of rainstorm collected in the run decreases as 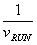 to a non-zero limit representing that volume of rain. It always helps to run faster. The function has no minimum.
to a non-zero limit representing that volume of rain. It always helps to run faster. The function has no minimum.
-
Contact Information
Contact Number: 717-871-4297
Email: physics@millersville.edu