Experiment of The Month

The MU Physics Department does not claim to have invented these labs. The origin of these labs is currently unknown to us. Our labs do not have written instructions. In keeping with this spirit, the description given here will be brief and general. The intent is that each performance of the lab will be unique; in each nature will reveal a slightly different face to the observer.

The site for this exercise is the kitchen of Dr. Nolan. Many have tried this experiment. Few have analyzed it. Because the analysis is the interesting part, we call it our

Problem of the Month

The other day, I wanted to suspend a calendar from a spring clip. The spring clip, in turn, was to be attached by magnet to a refrigerator, but the magnetic part of the problem is irrelevant. After placing the calendar in the spring clip, it became clear that the situation was unstable. Even the slightest jostling of the calendar made it slide out of the spring clip. What to do?

One simple solution presented itself. Place a shim ( more paper) between the calendar and the spring clip thereby increasing the tension in the spring and the frictional forces acting between the surfaces of the clip and the calendar. This worked. However, the shim also adds more weight to the system. If the density of the shim is too great, it could make the situation worse, not better. There is clearly a critical density involved here.

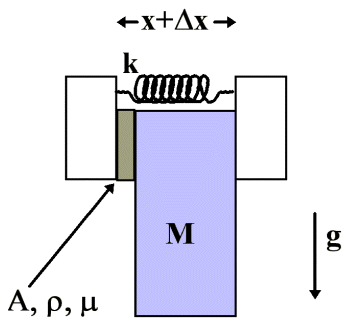
The diagram below schematically illustrates the situation before the shims are added.

The forces of friction between the clamp and the mass M must support its weight. If we denote the force of friction on either side as F then

(1)

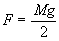
Furthermore, the force of friction must be less than the maximum provided by the static coefficient of friction and the normal force N.:

(2)

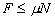
where m is the static coefficient of friction. The normal force is proved by the spring:

(3)

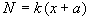
where k is the spring constant and a is reference length which determines the force of the spring when x, its extension, is zero.

Since the system of interest seemed to be on the verge of failure, we take the equality of Equ (3) and easily derive a relationship between the mass M, the spring constant k, the coefficient of static friction m and the lengths x and a.

(4)

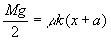
We now insert the shim of thickness D x, cross sectional area A and mass density r. The picture below summarizes the new situation.

We assume here the same coefficient of static friction m for all relevant surfaces. If the addition of the shim is to increase the stability of the system then we must have:

(5)

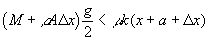
Combining Equs (4) and (5) we obtain

(6)

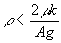
This defines a critical density . If the shim has a mass density above this critical density then the addition of the shim is counterproductive. If the shim is below this critical density then its insertion increases the stability of the system.