Experiment of The Month
Galilean Relativity
This June, the department conducted a summer workshop for 10 physics teachers on experimental evidence for Einstein's special relativity. The main evidence is the cosmic ray muon experiment, described in another edition of the Experiment of the Month. To appreciate the significance (and strangeness) of special relativity, we also did (low velocity) experiments that demonstrate "ordinary," or Galilean relativity.
Taylor and Wheeler (in Spacetime Physics, second edition, W.H. Freeman, New York, p53) summarize Galileo's discussion of the principle of relativity: "With shades
A discussion with a more algebraic flavor refers to two observers, A and B, who move with respect to each other at constant velocity: No experiment that A can do will reveal whether he is "really" moving or not. The same is true for B. The only thing that A and B can say is that they are moving relative to each other. As a result of their relative motion, A and B will record different descriptions of events that they observe. However, the differences in the descriptions will also fail to reveal who is "really" moving.
To experience Galileo's version, we used a small recreational vehicle, large enough to hold the participants. We pulled the shades down and did two projectile motion experiments: In one a marble was dropped 1 meter from the ceiling to the table in the kitchen area. In the other, a marble was launched horizontally, about 0.4 meters above the table.
In both experiments, the location on the table at which the marble landed was marked. The experiments were repeated several times at these unaccelerated speedometer readings: 0, 10, 20, 55 MPH. (These numbers represent velocities relative to the road.) For the dropped marble, a cardboard box was used to deaden the bounce.
They were also repeated while the vehicle was in circular motion, turning "to the right." The wheel was turned as far as possible, and the speed was 10 MPH, except for one measurement at 5 MPH. The small number of repetitions for the circular motion (accelerated) measurements represents a balance between the need for more data, the danger of car sickness in the driver, and the eventuality that someone would want to know just what was going on in the parking lot.
The entire set of results for the projectile motion are shown in the figure below.
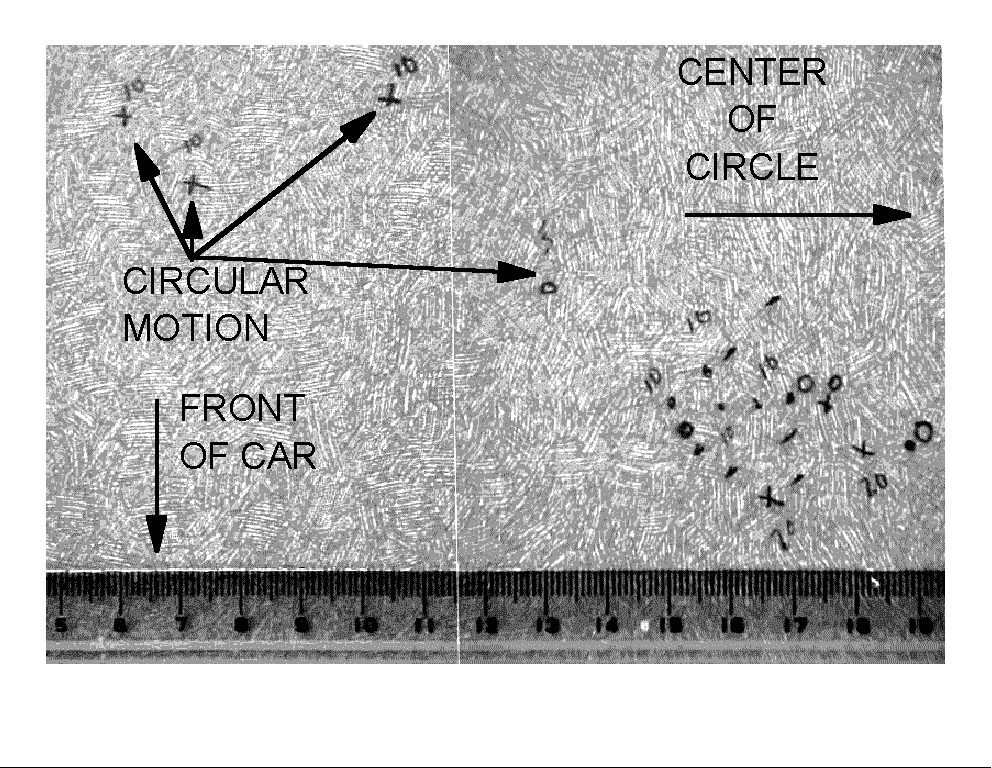
For unaccelerated motion, the landing dots cluster at the lower right of the figure. They are marked 0, 10, and 20 for the speedometer reading at which they were made. The 55 MPH data points are marked with a dash
For circular motion, the speed is constant but the velocity is not. This accelerated motion does produce observable changes in experimental measurements. Experiments now are the same as they would be if an artificial gravity were added to the earth's gravity. The magnitude of the "artificial gravity" is equal to the magnitude of the centripetal acceleration.
The artificial gravity direction is opposite to the centripetal acceleration of the van. In the figure, the center of the circle, and therefore the centripetal acceleration, is to the right. Thus the direction of the "artificial gravity" is to the left. It is this leftward artificial gravity that causes the landing spots for 5 MPH (only 1) and the 10MPH (3 of them) to shift to the left. Note that the 10 MPH spots are about twice as far from the constant velocity cluster as the 5MPH spot.
The results for the dropped marble are shown below. The landing spots are marked on a small cardboard box, which serves to deaden the bounce of the marble.

For constant velocity, the spots for speeds of 0, 10, 20, and 55 MPH cluster together, and mix. The spots give no basis for determining the speed of the van from the constant velocity marble drop experiment.
When the van moves in a circle at 10 MPH, the artificial gravity pulls the marble to the left, as indicated. (One marble landed out of the picture, 2 cm to the left, during the accelerated motion.)
The principle of relativity:
For all constant velocities, the outcome of these experiments is independent of the velocity of the vehicle relative to the road. The principle of relativity is upheld.
Analysis of accelerated cases:
In Galilean relativity, analysis is made easier by the fact that the vertical and horizontal components of the motion separate. Also, in Galilean relativity, all observers agree on the time. Thus, the time for the marble to fall to the table from the horizontal launch is the same, no matter what else is going on. The same is true for the time of fall from the ceiling to the table.
The dropped ball falls about 1 meter, and the launched ball falls about 0.4 meter. For a ball falling from height, h, the time of fall is given by
t2 =2h/g
In the horizontal direction, the only acceleration is the "artificial gravity," a. Because of this, the shift in landing position between constant velocity experiments and the circular motion (accelerated) experiments is calculated by simply adding an extra, "acceleration term," 1/2 a t2 . Using the time of fall to calculate the shift when the marble hits the table, we find a shift of
x = h(a/g)
When the acceleration, a, doubles, the shift should double. This is in agreement with the difference in landing point for the 5 MPH and 10 MPH circular projectile measurements.
When the height doubles, the shift should also double. The equation does not agree well with the difference between the drop from 1 meter and the launch from 0.4 meter above the table. The shift for the 1 meter drop is larger than the shift for the 0.4 meter projectile, but it is not twice as large, as the equation predicts.