Experiment of The Month

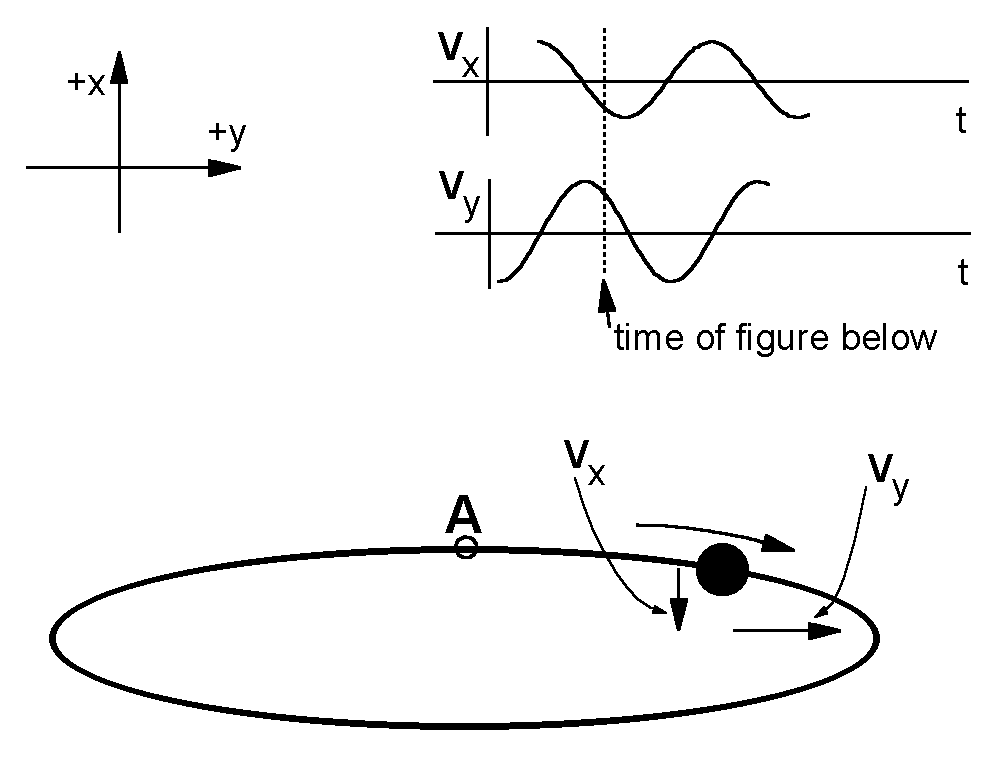
Looking down on the pendulum, as in the figure , the simplest motion of the pendulum bob would be motion in a straight line. (Strictly, the projection of the pendulum motion onto a horizontal plane can be a straight line.) The pendulum motion can also create an ellipse in the horizontal plane.

The ellipse may be described as the sum of two motions, one along the minor axis of the ellipse and one along the major axis. Ordinarily, the bob displacement along the minor axis is maximum when the bob displacement along the major axis is zero.

In the figure at right, the major axis is along the y axis, and the bob is following a clockwise path around the ellipse.

Ordinarily, it is assumed that the period of a pendulum is independent of the amplitude of the pendulum motion. In the case of elliptical motion this means that the period of oscillation along the minor axis (x) is the same as the period along the major axis (y).

Imagine for a moment that the period along the x axis is made shorter than the period along the y axis. In particular, imagine that the period becomes shorter just as the bob passes through point A. After 1/4 of a period, the bob will go to its maximum y displacement (zero y velocity). Ordinarily, at the same time, the bob will reach zero x displacement (maximum x velocity).

However, if the x period is shorter, the x motion reaches its maximum velocity sooner. Its average velocity during this 1/4 period is larger, and the bob travels farther during the 1/4 period than it "should." The effect of this extra travel in the x direction is to shift the apse of the ellipse in a clockwise direction.

In fact, the period does depend (weakly) on the amplitude of the motion, and the minor axis does have a shorter period. If the bob follows a clockwise path around the ellipse, the ellipse will precess clockwise. The larger the difference in periods, the larger is the rate of precession. To minimize this effect, in monumental Foucault pendulums, the amplitudes are kept small.

Synge and Griffith worked out the rate of precession for their mechanics book. (Synge and Griffith, Principles of Mechanics, McGraw-Hill, second edition 1949, 373-381)

Their result, and an application to a pendulum like ours is shown in the figure at the right. In the figure Xmax is the maximum displacement along the minor axis, and Ymax is the maximum displacement along the major axis.

The ordinary Foucault pendulum at our latitude (about 40 degrees north) "should" precess clockwise at about 10 degrees per hour, roughly 0.2 radian per hour. This is the same as the elliptical precession when the minor axis is only 2% of the major axis in size.

The bob can follow an elliptical path in either the clockwise or the counterclockwise direction, leading to precession either in the direction of the Foucault precession, or opposite to it.

Our method of driving pumps energy into the major axis motion, and pumps energy out of the minor axis motion. In the absence of the Coriolis force, our pendulum motion would evolve towards linear motion rather that elliptical motion.

On the other hand, in the presence of a Coriolis force, our method of driving causes a clockwise precession. A sketch of how the Coriolis force associated with the vertical driving velocity induces clockwise precession follows:

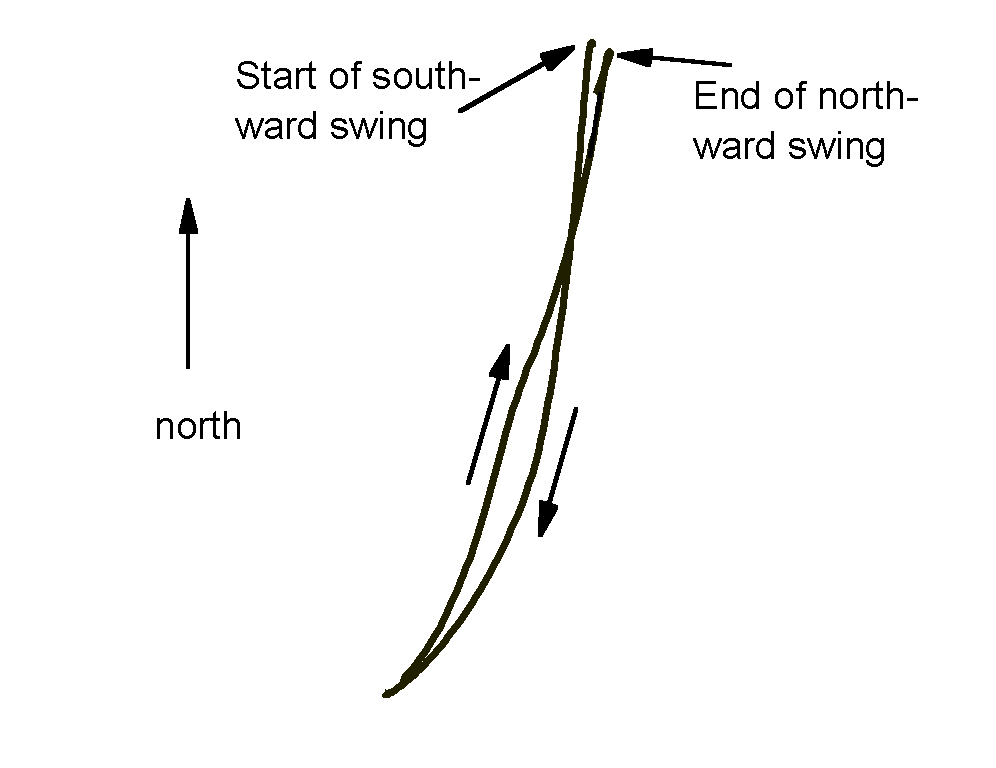
At mid-latitudes, when pendulum is pulled up as the y axis swings north at maximum velocity, the vertical component of velocity causes the bob to move (more nearly) parallel to the earth's axis. The Coriolis force is reduced.

When the same bob swings south, pulling the bob up causes the bob to move (more nearly) perpendicular to the earth's axis. The Coriolis force is increased.

In the extreme case, the northward path is straight, with no Foucault precession, while the southward path is curved, with an enhanced Foucault precession. This cyclic path has an elliptical component, with clockwise elliptical trajectory.

The piston driven pendulum will precess clockwise more rapidly than the Foucault pendulum, because of the additional elliptical precession, driven by the Coriolis force on the vertical pumping motion.

In the figure at the right, the path of the bob is calculated for one cycle, 2 seconds in duration, as the bob swings first south, and then north. The drive is a 0.1 second upward pull at the lowest part of the northward swing. The north-south motion is assumed to be sinusoidal. The east-west motion is due to the Coriolis force.

In the figure, the end point has shifted clockwise from the starting point due to the ordinary Foucault precession. The path has opened to approximate an ellipse, due to the modification of the coriolis force by the additional velocity caused by the vertical driver.

To make the effect easier to see, it has been exaggerated by stretching the picture along the x axis.