Experiment of The Month
A Holiday Measurement of Earth's Circumference
Thanks to Gregor Shapiro for corrections to this article.)
Credit for the first estimate of the Earth's radius goes to Eratosthenes, in Alexandria, around 240 B.C.E. As recounted by Alder (Ken Alder, The Measure of All
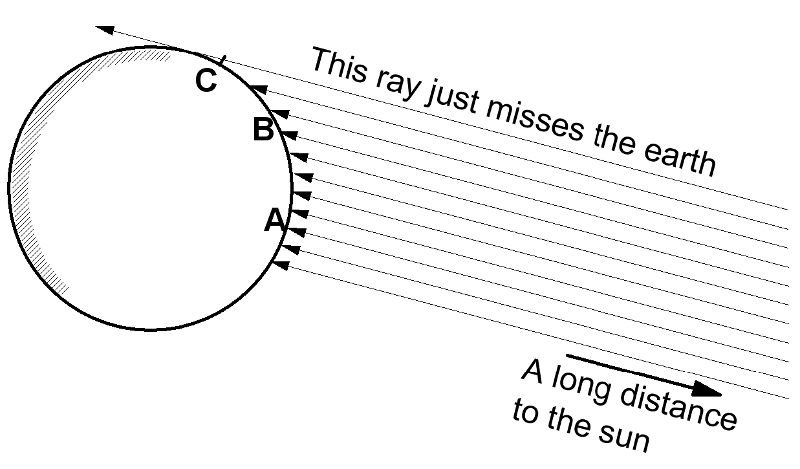
Eratosthenes analyzed the observations with the assumption that the earth is a sphere and the sun is very far away. The geometry of the situation is sketched at the right. He concluded that the circumference of the earth was about 50 times greater than the distance from Alexandria to Aswan. His results and modern results agree within about 10%.
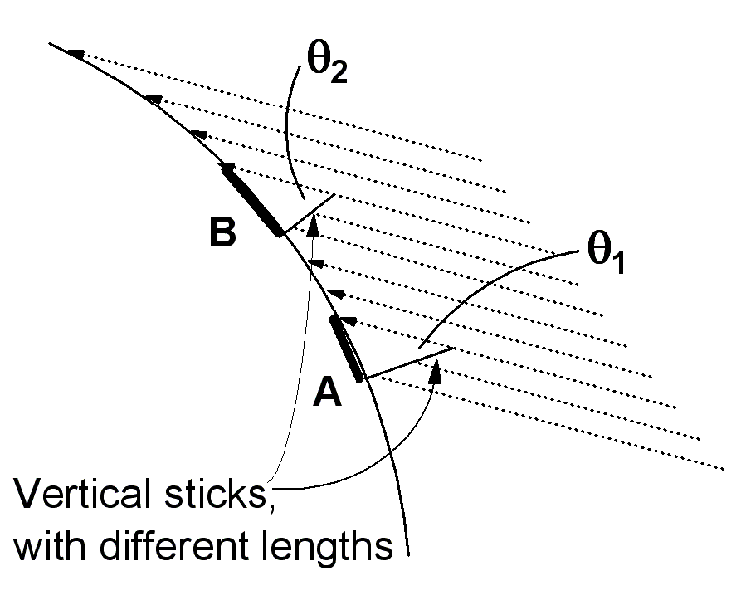
Because the sun is assumed to be very far away, we believe that the light rays which reach us from the sun are all going in the same direction; they are parallel. (This assertion can be tested by observing a beam of light from the sun which passes through a 1mm hole in a large piece of cardboard.) In the figure, a vertical stick at point A would cast no shadow, a stick at B would cast a "moderate" shadow, and a stick at C would cast a very long shadow.
In Eratosthenes' experiment, A would correspond to the well at Aswan, on the day of the summer equinox, and Alexandria would be located somewhere between A and B.
U.S. Route 95 runs all the way from Maine to Florida. Anyone with access to Route 95 and a tape measure can repeat Eratosthenes' measurement, and can even use a baseline that is longer than his.
Over the winter break, on a trip to Florida from Pennsylvania, the author had the opportunity to repeat these measurements. The measurements were done near the winter
A tape measure was used for the "vertical stick" and a carpenter's level with an inch scale on top was used to measure the length of the shadow. In the picture above left, the
In the figure above right, a smaller segment of the spherical earth's surface is shown, with the light rays now shown as dotted lines. Location A represents Florida, and location B represents Pennsylvania. The shadows are represented by heavy lines parallel to the earth's surface. The stick at A is longer, but the short stick at B casts a
 The measurements will be discussed in terms of the angle that a
The measurements will be discussed in terms of the angle that a
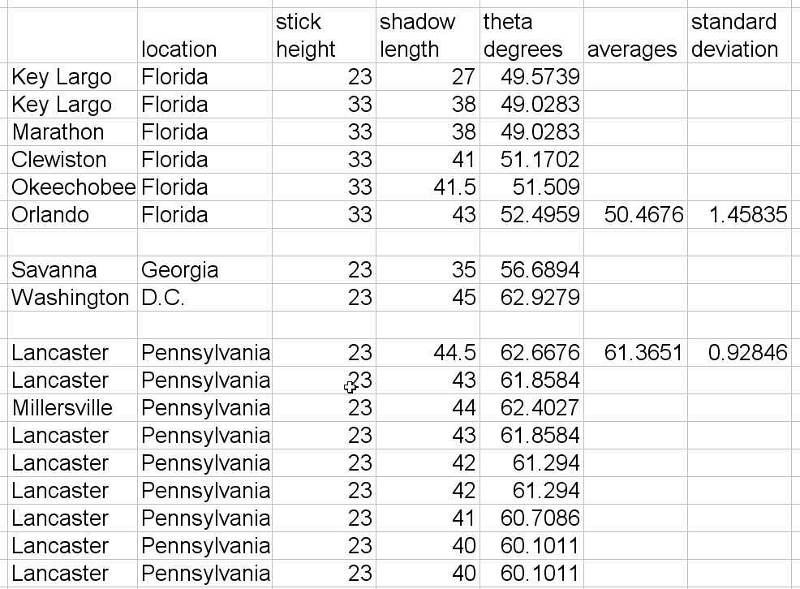
The table at the right shows the results. Each entry is for noon on a different day, and the table is ordered with the earliest day at the top. The 17 data points were taken over a period of 24 days. The average shadow angle for Florida has a fairly large standard deviation, partly because measurements were taken at a variety of locations, from Orlando to the Keys. The standard deviation of the Lancaster data must have some other cause.
Taking the averages at face value, we can say that the difference in sun angle between Florida and Pennsylvania is about 10 degrees, with an uncertainty of about 2 degrees. The odometer reading on the car showed 987 miles traveled between the northern edge of Florida and Lancaster, Pennsylvania. The separation of those two locations is smaller, of course, and the average distance to the more southerly Florida locations is larger. We can estimate the separation of the two averages at 1000 miles, with an uncertainty of perhaps 100 miles.
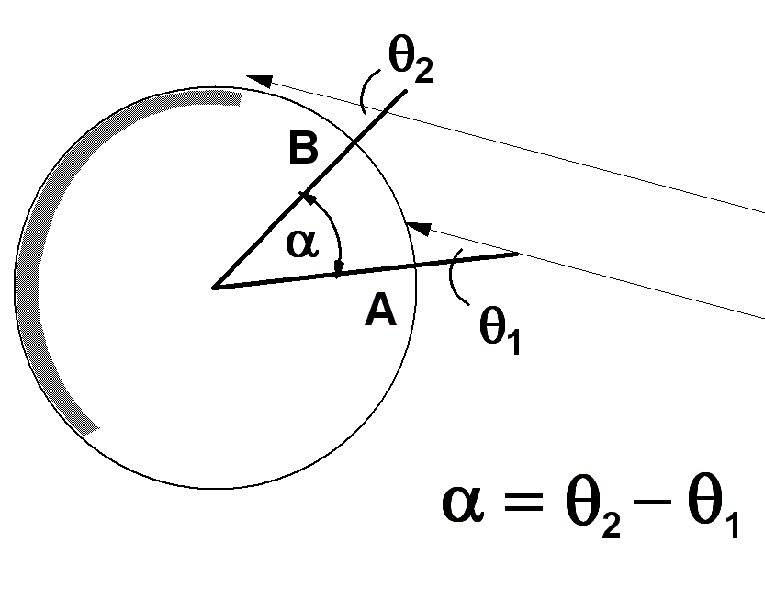 The relation between the shadow angle and the angular location on the earth is sketched in the figure at the right. The angle defined by the shadow is the same as the angle between a sun ray and a radius line of the earth. The two angles @1 and @2 are at locations A and B in the diagram, respectively.
The relation between the shadow angle and the angular location on the earth is sketched in the figure at the right. The angle defined by the shadow is the same as the angle between a sun ray and a radius line of the earth. The two angles @1 and @2 are at locations A and B in the diagram, respectively.
The diagram shows the earth radius which leads to point A and another leading to point B. A little geometry shows that the difference between the shadow angles is the same as the angle between those two radii. In our case, the shadows tell us that we have moved about 10 degrees around the earth when
This rough agreement with other measurements of the circumference encourages us to analyze the data more carefully.
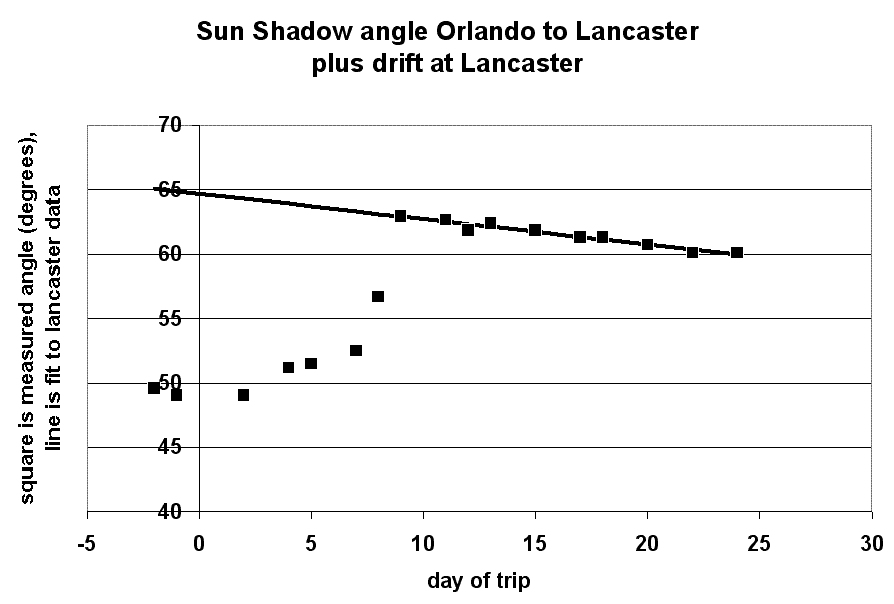 The plot at the right shows the shadow angle plotted versus the day on which the measurement was made. Day -2 represents December 30, 2002 (in Key Largo, Florida), and day 24 represents January 24, 2003 (in Lancaster, Pennsylvania). We worked our way north from the Keys through Orlando. Day 7 was the last Florida measurement, and day 11 was the first Pennsylvania measurement. Day 8 was in
The plot at the right shows the shadow angle plotted versus the day on which the measurement was made. Day -2 represents December 30, 2002 (in Key Largo, Florida), and day 24 represents January 24, 2003 (in Lancaster, Pennsylvania). We worked our way north from the Keys through Orlando. Day 7 was the last Florida measurement, and day 11 was the first Pennsylvania measurement. Day 8 was in
The Lancaster measurements show a definite trend, indicated by the solid line. The shadow at Lancaster is getting longer as the year progresses towards spring and the sun rises in the sky. By extending the solid line back in time, we can estimate the shadow angle in Lancaster when we were measuring the shadow in southern Florida. The graph suggests that 15 degrees
With 15 degrees corresponding to 1000 miles, we estimate the circumference of the earth at 24,000 miles, in better agreement with published results.
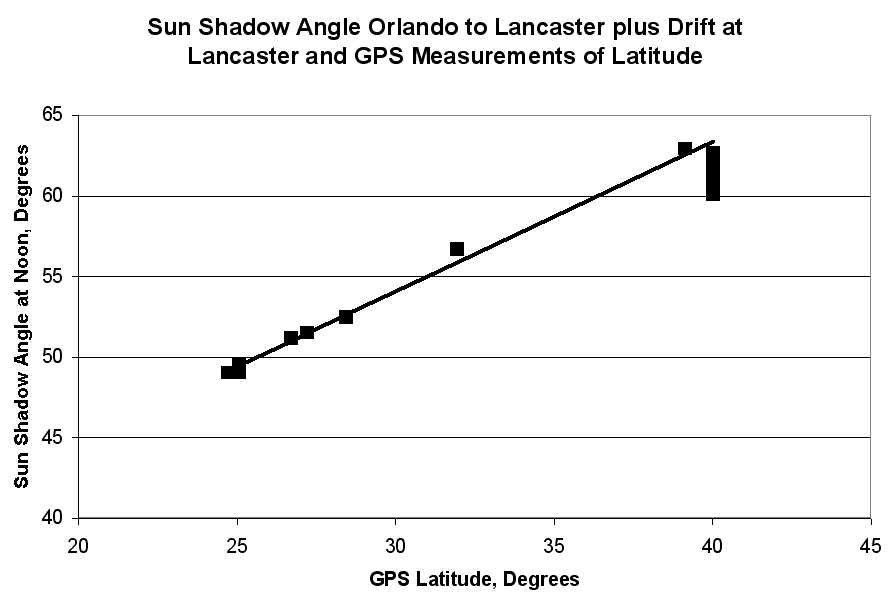 Finally, we note that the angular difference between the shadows at two points, A and B, is the same as the difference in latitude between those two points. Thus the shadow angle should change in direct proportion to the latitude at which the measurement was taken. A plot of shadow angle versus latitude should have a slope equal to 1. Such a plot is shown at the right
Finally, we note that the angular difference between the shadows at two points, A and B, is the same as the difference in latitude between those two points. Thus the shadow angle should change in direct proportion to the latitude at which the measurement was taken. A plot of shadow angle versus latitude should have a slope equal to 1. Such a plot is shown at the right
As indicated in the figure, the latitude was measured with a hand-held Global Positioning System receiver. the straight line is a fit to the first 9 measurements, including only the earliest measurement at Lancaster.
The slope of the line should be 1. It is .93, with an uncertainty of .03. The lower than expected slope is probably associated with the shortening shadow, as the days went by. With this caveat, we can say that the agreement between shadow angle and GPS latitude is good.
On the day of the winter solstice, ( a few days before our earliest measurement) the difference between the shadow angle and the GPS latitude is the same as the angle at which the earth's axis is tilted relative to its plane of orbit. The difference between the shadow angle and the GPS latitude is also equal to the intercept of the straight line in the graph. This intercept is 26 degrees with an uncertainty of 1 degree. That result agrees roughly with the official angle of tilt of the earth's axis, 23.5 degrees.
An Alternative Model
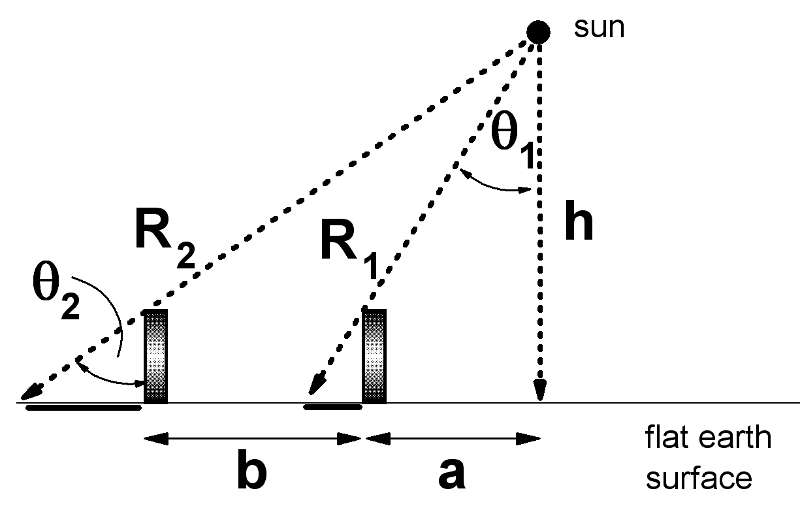 Eratosthenes' model depends on the assumption that the sun is far away and therefore produces parallel rays of light all over the earth. If the sun is nearby, then shadows will change length even for a flat earth. A flat earth model is sketched at the right. The vertical stick casts shadows that grow longer as the stick moves to the left, away from the closest point to the sun. (The sun is at height h above the earth.)
Eratosthenes' model depends on the assumption that the sun is far away and therefore produces parallel rays of light all over the earth. If the sun is nearby, then shadows will change length even for a flat earth. A flat earth model is sketched at the right. The vertical stick casts shadows that grow longer as the stick moves to the left, away from the closest point to the sun. (The sun is at height h above the earth.)
A little trigonometry shows that
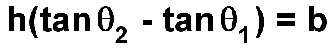
Using the values 50 degrees and 60 degrees as measured on the trip, with b=1000 miles, we find that
Continuing the calculation, we find that a is approximately 2400 miles and the two distances R1 and R2 are approximately 3000 and 3900 miles, respectively.
That is, as we move from Florida to Pennsylvania, our distance from the sun increases by about 30%. As a consequence, the apparent size of the sun should decrease by 30%. We see no noticeable change in the apparent size of the sun as we make the trip. We conclude that the flat earth/near sun model does not work.