Experiment of The Month

For his senior seminar, Matt Panas studied the refraction of light by the density gradient in a chamber full of freon. In the process of working out the theory with his advisor (Dr. Miziumski) he showed us an interesting variation on deriving Snell's law. His approach made his subsequent analysis easier to do. We will focus here on the simple laws for reflection and refraction.

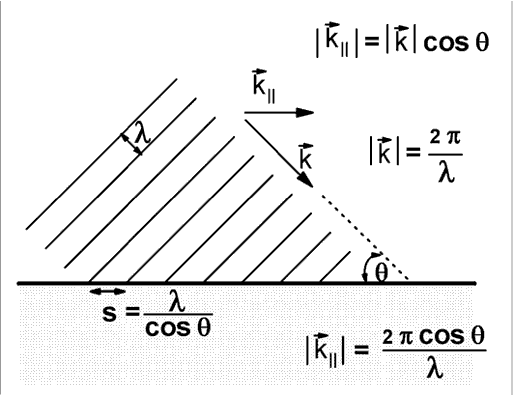
The figure above shows a wave, of wavelength l (lambda) approaches the interface between two different media. The interface is represented by the heavy horizontal black line. The wavelength is measured as the shortest distance between adjacent wave crests. This distance is measured along a line that is perpendicular to the wave crests, and parallel to the direction of propagation of the wave.

The wavelength, l, is a natural way to characterize the periodicity of the wave in space, much the same as the period, T, is a natural way to characterize the periodic motion of a simple harmonic oscillator. For oscillators, it has become common to describe the motion by a frequency, f = 1/T instead of the period, T. The frequency tells us how many oscillations occur in a unit of time. We use the idea for motors (RPM), sound pitch, radio tuners, and computer speed (Hertz = cycles per second).

Less common is a "spatial frequency" defined as 1/l. A measure of the low status given this parameter is that its units have not been assigned to a dead physicist. The spatial frequency tells the number of wave crests per meter.

In the analysis of oscillators, it is often convenient to replace the frequency, f, with a "circular frequency" w= 2pf = 2 p/T. Since 2p also represents the number of radians in a complete circle, the units given to w are radians/second.

For analysis of many wave problems, including the present one, a spatial imitation of w is defined,
k = 2 p/l
Evidently the units of k are radians per meter.

This parameter, the "wave vector" is given additional work by assigning it a direction which is the same as the direction of travel of the wave crests. We think of the k-vector as having the same direction as the wave velocity. In the figure above the arrow above the letter k represents the vector (directional) character of the k-vector. The figure shows both the k-vector and a natural second idea: a component of the k-vector called k_|| .

The subscript _|| means "parallel" because the component shown is parallel to the interface between the two different media in which the wave is to propagate. The figure shows two different ways to calculate k_||. The first (upper) is the usual projection using the cosine of the angle between the vector and the parallel direction. The second (lower) requires more discussion.

When a crest strikes the interface, the point of contact sweeps along the interface to the right in the figure. The distance between the contact points for two successive wave crests is called "s" in the figure. A little trigonometry shows that
l/s = cos q where the angle theta (q) is the angle between a wave crest and the interface.

The periodic array of intersection points has a repeat distance, s. We can associate a k-vector along the surface with this periodic structure, k_||= 2 p/s

The two different methods give the same value for k_||

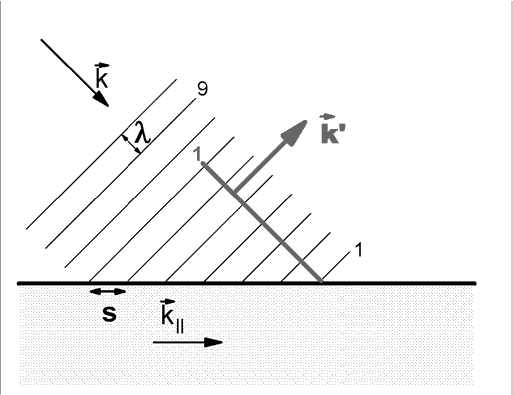
The figure above shows one extra wave crest; a crest that was reflected at the interface. We think of this reflected wave crest as being generated by the interface, at the point where the incoming wave strikes the interface. We have named the incoming crest, and its descendent "1."

Because the reflected wave crests are generated by the incoming wave with a well defined frequency (in time), f, the reflected wave will have that same frequency. Since the reflected wave travels in the same medium as the incoming wave, it has the same wave velocity magnitude. As a result, the reflected wave has the same wavelength as the incoming wave.

The reflected wave vector, k' is different in direction from the incoming wave vector, k, but the magnitudes of the two are identical.

The figure below shows two of the reflected wave crests, named 1 and 2.

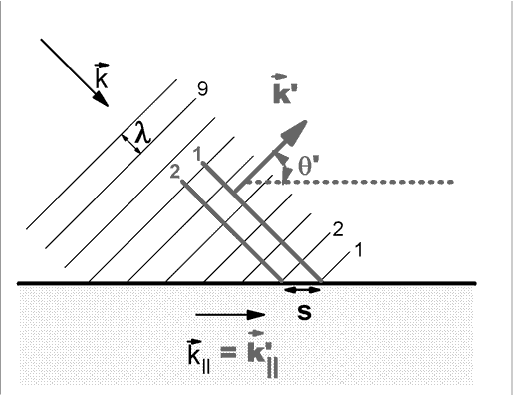
Since the points of intersection of the incoming wave with the interface are the launching points for the reflected wave, we se that the distance s is the same for both the incoming wave and the reflected wave. But this means that k_|| is the same for both waves: k_||=k'_||. If the two k-vectors have the same magnitude and the same component parallel to the interface, then they must make the same angle with the interface: q' = q .

That is, the angle of incidence equals the angle of reflection.

Finally, we are ready to use this picture to establish Snell's law.

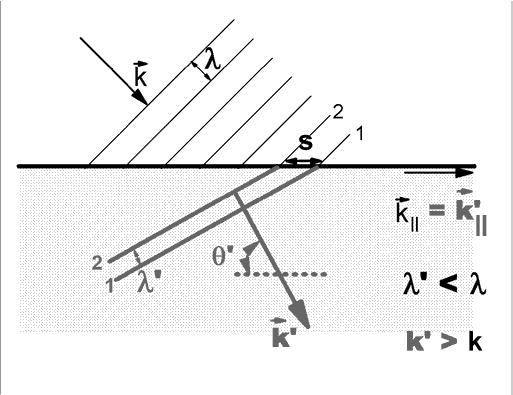
Now we imagine the point of contact between an incoming crest and the interface as the source of a wave launched into the second medium. The picture assumes that the wave velocity is slower in the second (shaded) medium. The new wave has the same frequency, f, as the original, because it is generated by a disturbance at the interface with that frequency.

The new wave also has the same parallel component of k-vector, since that is determined by the distance s in the figure. However, the new wavelength is shorter, because the velocity is slower (and the frequency is the same).

This means that the new k-vector is larger in magnitude than the original. To meet both the conditions (larger magnitude and k_||=k'_||) the angle of the outgoing k-vector must change:
k' cos q ' = k cos q or
(k'/k) cos q ' = cos q

Since k-vector magnitude is inversely proportional to the wave velocity, and the velocity ratio is defined to be the index of refraction, n, we have
n cos q ' = cos q

Traditionally the angle used is the angle between the k-vector and the normal to the surface. In that case the cosine function is replaced by the sine function, and we have the traditional form of Snell's law.