Experiment of The Month
Interferometric Measurement of Glass Thickness

This is an exercise for our advanced laboratory students, to introduce them to our better optical equipment. The instructions are to use light interference to measure the thickness of a glass slide. Students set up a Michaelson interferometer, as at the right, using a HeNe laser. The mirrors were not set to form the familiar bulls-eye pattern shown here. Instead, one mirror was tilted to show a straight line fringe pattern, visible in the photo at the right.
Light comes in from the laser at the right, passes a lens and enters a beam-splitter. Half the light comes towards us and half proceeds to the left from the beam splitter. Both beams are reflected back. Half the light from each beam proceeds away from us to hit the screen and form the interference pattern.
The microscope slide is inserted into the beam traveling toward us (and also away from us after reflection). Because the speed of light is slower in the glass, light passing through the glass travels a greater number of wavelengths than it would with the glass removed. This extra delay in our path shifts the fringe pattern on the screen because different wave crests are now adding in phase from the two beams.
The microscope slide is mounted on a rotating stage. The experiment is begun with the slide perpendicular to our light beam. When the stage is rotated, the light travels an even longer path through the glass, as illustrated in the sketch below.
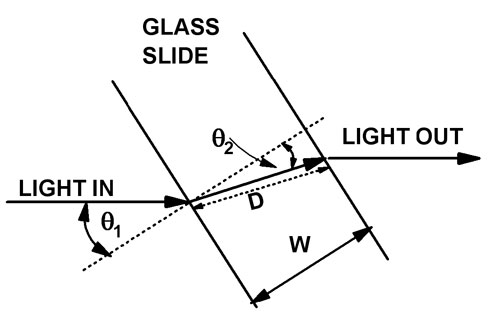
The distance, D, traveled by the light beam in the glass, is related to the thickness of the slide, W, by
W/D= cos q2
If the index of refraction of the glass is n, we can use small angle approximations to reach this description of the distance, D:
D ~ W(1+[q1/2n]2 +...)
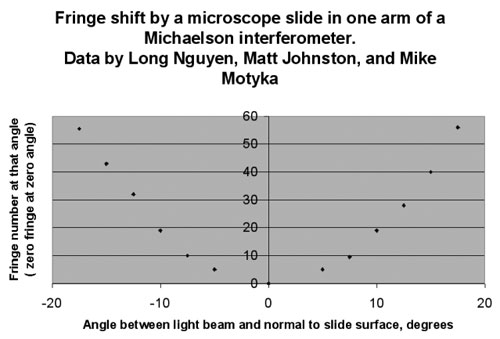
Every time D increases by 1/2 wavelength, the fringe pattern will shift by 1 fringe. (We neglect for now the change in path length through air caused by changing q1.) Counting the number of fringe shifts, m, with m=0 when the incoming light is normal to the slide, m will be quadratic in the angle q1
A plot of m versus q12 should have a linear slope, which can be used to determine W from the known wavelength of the light
SOME DETAILS
To calculate the thickness of the glass slide, taking into account the fact that the length of the light path through the air also changes when the slide is rotated, we need to look in detail at the geometry.
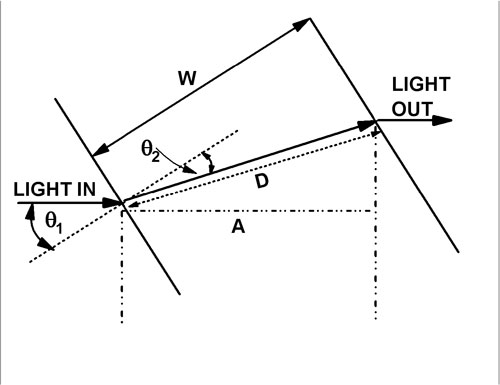
D is the distance light travels
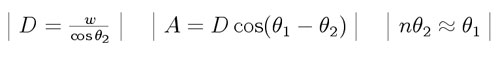
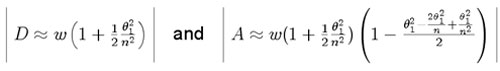
Writing out A,
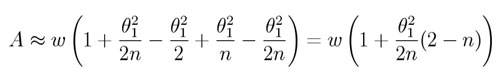
When the slide is inserted into the Michaelson light path, replacing a path, A, of air, the change in optical path length is
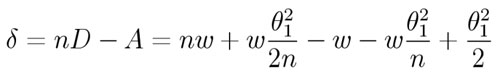
or
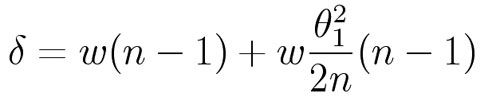
Setting the path length equal to
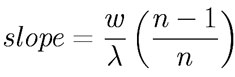
so that
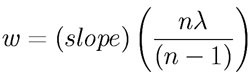
-
Contact Information
Contact Number: 717-871-4297
Email: physics@millersville.edu