Experiment of The Month
When Equipartition of Energy Does Not Work
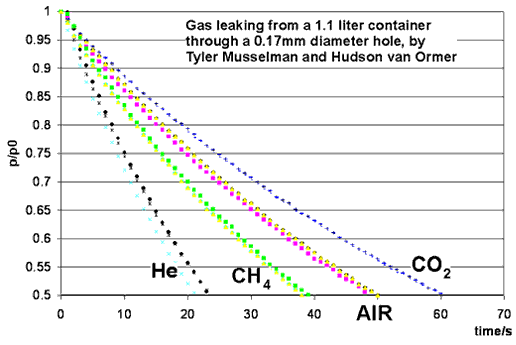
This month's experiment is performed by students in the Chemistry Department's physical chemistry course, taught by Dr. Iannone. Students were Tyler Musselman, Hudson van Ormer, Ian Rowe, Kelly Rhoads, Anthony Burkholder and Erik Allman. A small hole is opened in a container of gas, and the pressure of the gas is measured as a function of time. The ideal gas laws give an excellent prediction for the rate at which gas leaks out, provided that the average velocity of gas molecules is correctly calculated.
The figures below show enlarging views of the opening and the trajectory of an escaping gas molecule.
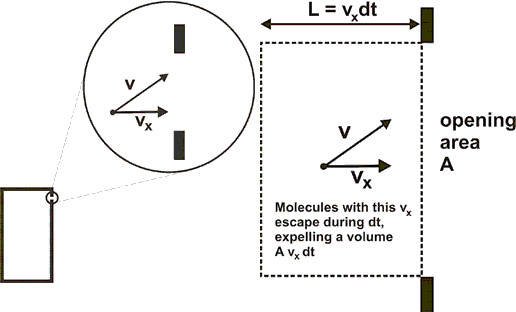
Velocity component
dN=(r)(Avxdt) move out of the volume. (r is the number of molecules per unit volume.)
The rate at which molecules with this
If that is the average velocity component, we can use it to estimate the average rate at which molecules leave the volume. We can find the average velocity component in terms of in terms of temperature, T, in two interesting ways.
The naive approach is to refer to the equipartition of energy, stating that each degree of freedom of a molecule carries, on average, 1/3 of the total energy of the molecule. That is, m <vx2>=kT
where m is the mass of the molecule and k is Boltzmann's constant, and the <> brackets indicate the average value of vx2. Naively, we can set
vx=(kT/m)(1/2).
However, for this
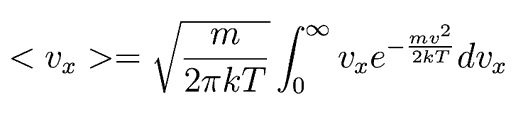
Following Hyperphysics pages for these kinds of integrals, we can find
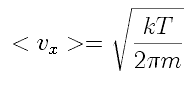
This integrates
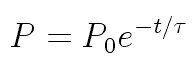
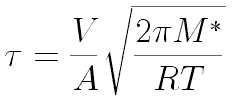
Dr. Iannone's students Ian Rowe and Kelly Rhoads measured 90 seconds
When the naive value for
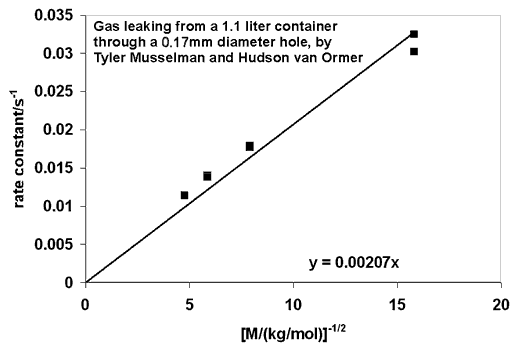
The graph below shows the rate constant (k = 1/t) versus 1/(square root of molecular weight) for the data graphed at the top of the page. The results indicate that t does indeed depend on the square root of the molecular weight, as predicted. They also hint at a discrepancy for helium, the pair of points farthest right on the graph. It would be interesting if the long mean free path of helium molecules were being reflected in the data.