Experiment of The Month

In our second experiment of the month, we reported that our measured capacitance for electrolytic capacitors was consistently higher at dc than at audio frequencies. This month's experiment reports on measurements to clarify the situation. When it came time to choose his senior project, senior physics major Ed Tangradi remembered his physics 2 experiment and decided to follow up by measuring capacitance as a function of frequency.

His circuit is shown in the figure.

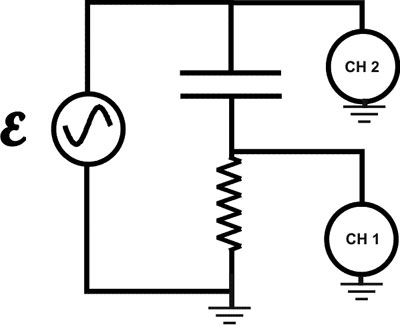
The resistor is used to determine the current with channel 1 of the oscilloscope. Its resistance is 3.3 Ohms. Channel 2 measures the emf across the RC circuit. From the amplitudes of the two readings and the phase difference, we can determine the capacitance and the power absorption of the capacitor, as a function of frequency, w.

The relations we need are in the figure below. The capacitance is proportional to the dielectric constant, K.

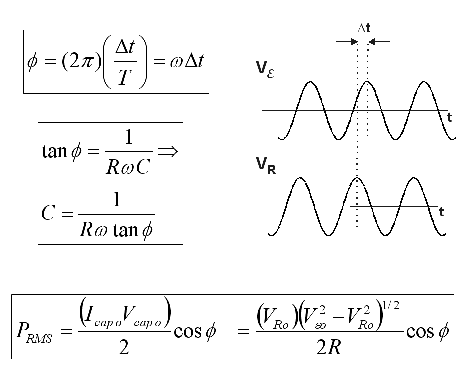
The idea for the analysis is that the dielectric constant of the dielectric material in the electrolytic capacitor is due to rotating dipoles. (The theory also applies to induced dipole moments, but rotating dipoles are easier to visualize.)

The dipoles together as a group produce the polarization of the material. The ratio of the polarization to the electric field, E, determines the dielectric constant. In MKS units, the dielectric constant, K, is

If the dipoles are rotating in a viscous medium, the torque applied by the electric field to the dipole determines the angular velocity, rather than the angular acceleration. (It is assumed that the motion reaches terminal velocity quickly.)

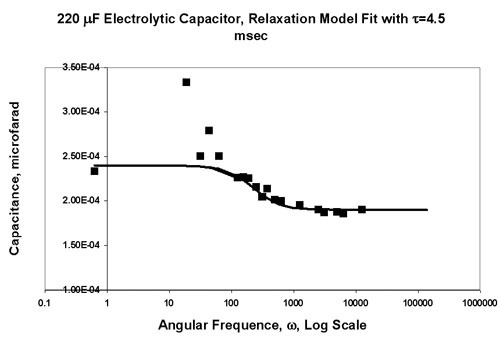
The viscosity causes the orientation to lag behind the applied electric field. At very low frequencies the lag is not noticeable, but at higher frequencies, the polarization does not have time to relax to the value it would have for a static electric field. The result is lower measured capacitance.

In a perfect capacitor, the velocity of the rotating dipoles is 90 degrees out of phase with the driving torque, for a sinusoidal applied EMF. This means that the net work per cycle on a dipole is zero. When the dipole motions lags due to viscosity, the phase angle changes and the net work on the dipole per cycle is positive. The energy delivered to the dipole is in turn dissipated by the viscous force.

The theory for this problem was worked out by Debye and described by Kittel (1956 Introduction to Solid State Physics, Wiley, pp 174-179). A more directly applicable discussion is "Dielectric loss due to polar molecules in solid paraffin wax" by D. R. Pelmore, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 172, No. 951, (Sep. 4, 1939), pp. 502-517, available by googling "dielectric loss in solid paraffin."

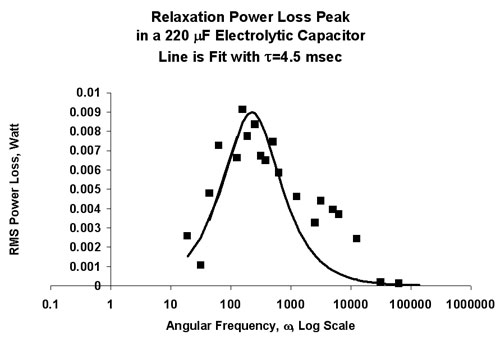
Pelmore uses the Debye result that the power loss is:

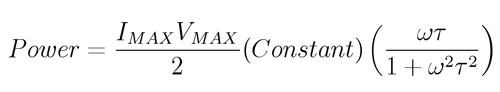
where t is the characteristic relaxation time for the dipoles in the viscous medium. The capacitance is:

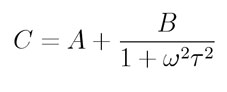
Some results for power loss and capacitance as a function of frequency, along with a fit to these two functions, with relaxation time t = 4.5msec are shown below. The magnitude of the capacitance effect is consistent with that described as "soakage" in this Wikipedia article.