Experiment of The Month
Origin of Bending equation
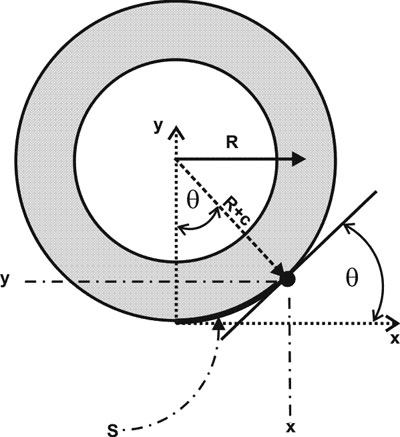 The fundamental equation used to analyze beams
The fundamental equation used to analyze beams 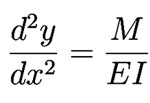

where the integral is over the
To glimpse the origin of this formula, imagine a rectangular beam bent (gently) into a circle of radius R. In the figure, c is the distance from the beam center (strictly the centroid) to the outer edge of the beam. A point on the outer edge is marked with a dot, a distance R+c from the center.
In
For small x, the angle theta can be related to the derivative of y with respect to x for the outer edge of the beam.
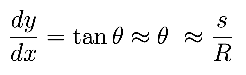
We eliminate R from this expression by considering the strain induced in the outer edge of the beam when it is flexed into this curved shape. In bending, the inner edge of the beam is compressed, the outer edge is stretched, and the centroid is unchanged in length. The strain in the outer edge is:
so that: 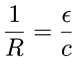
This
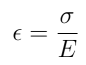
Using the result 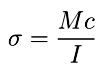
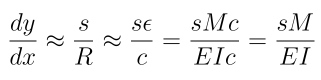
Now enforce the requirement that s be small. In that case, s is the same as x, and in particular
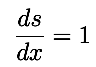
Taking the derivative of both sides of the
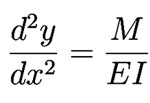
-
Contact Information
Contact Number: 717-871-4297
Email: physics@millersville.edu