Experiment of The Month

During a demonstration for a special topics course on ultrasonics, we needed to remove a 1 MHz signal from a 10 MHz signal. It seemed that a twin tee filter might do that job. It turned out that the filter was not needed. However, in the process we could not find an expression for the twin tee transfer function on the web.

The transfer function is derived here. The analysis is a nice example of the efficacy of complex notation for ac circuit problems.

The Twin tee filter circuit is shown below. VA is the input ac voltage. VB is the output voltage into an infinite impedance (so that the output current is zero). On the right is a realization of the filter, The 4 resistors are all color coded as 75 Ohm. The four capacitors are labeled as .0022 microfarad. Two resistors in series form the top of one tee. Two capacitors in series form the top of the other tee. The legs of the two tees, made from parallel combination of two capacitors and two resistors, respectively. The legs terminate in ground, represented by the paper clip.

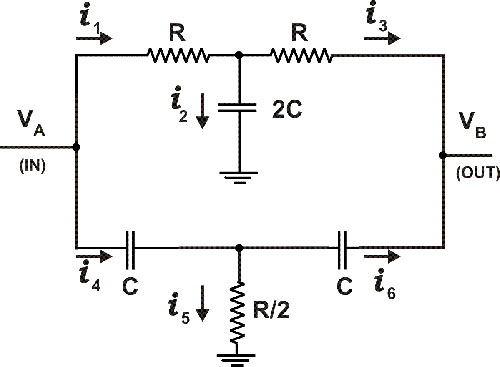
Taking for the input voltage

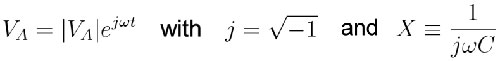
the result for the transfer function is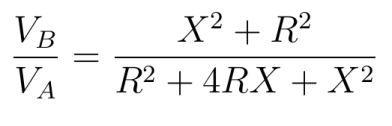

We derive this starting with four Kirchhoff loop equations:

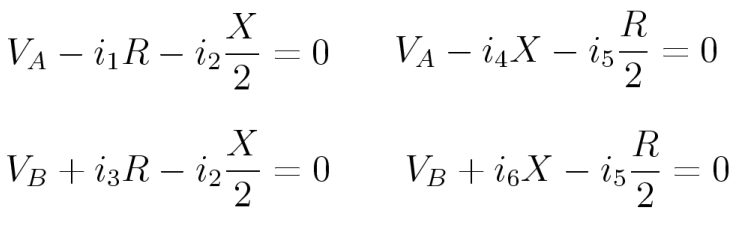
Three current equations are:

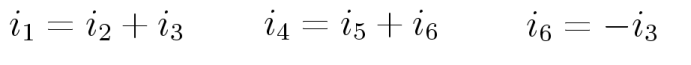
Use these currents to rewrite the loop equations:

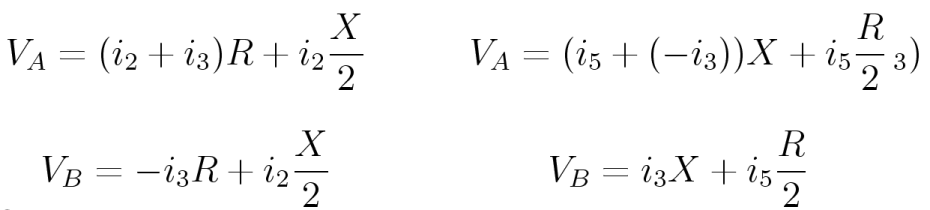
To simplify the math, add the two left equations and set the result equal to the sum of the two right equations. The result is surprising:

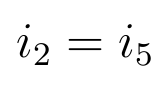
ALWAYS.

The four loop equations reduce to:

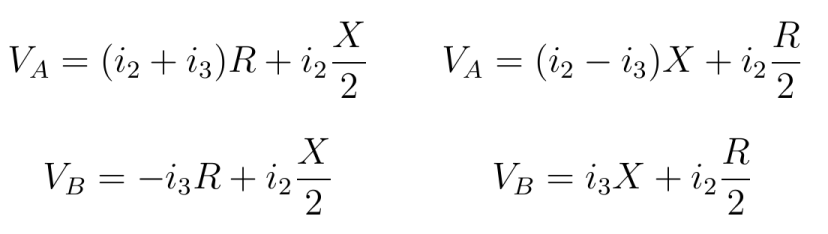
The two equations for VB imply that:

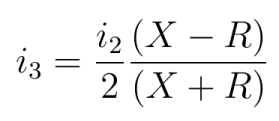
Replacing i₃ in the equations, we have:

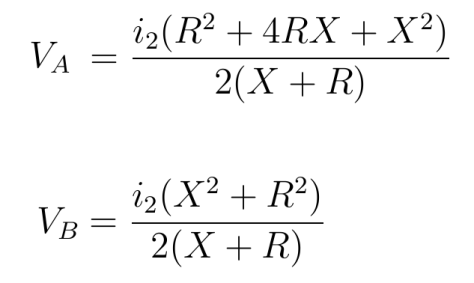
so that the transfer function is:

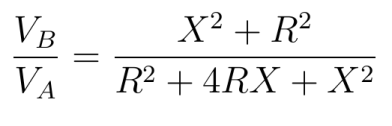
Recall that X is imaginary, so that the numerator is zero when RwC =1

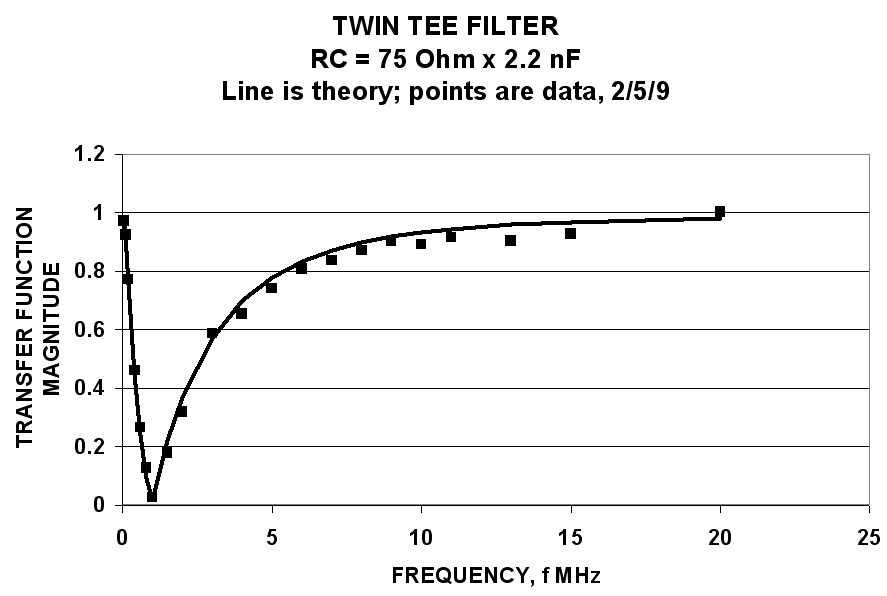
A graph of the theoretical transfer function is shown below (no adjustable parameters), along with data from a filter using the nominal for R and C.