Experiment of The Month
Independent Variables
Dr. Richard Clark of the Millersville University Department of Earth Sciences pointed out (private communication) that in our previous edition of the Experiment of the Month, the error propagation discussion (following http://mathworld.wolfram.com/ErrorPropagation.html) assumed that the variables were independent. He noted a more sophisticated method that allows calculation using variables which are not independent of each other.
The real world often demands such sophisticated analysis. However, physics education typically seeks to pick simple
Sometimes we are surprised to discover that two variables (which we expected to be independent) are not independent after all. We say that those two variables are "coupled." An example of coupling between important variables is illustrated by the pair of pendulums in the photograph. The two pendulums are identical. A description of a single pendulum behavior gives the angle made by the string (with respect to the vertical direction) as a function of time. The motion is determined by the force of gravity and the length of the string.

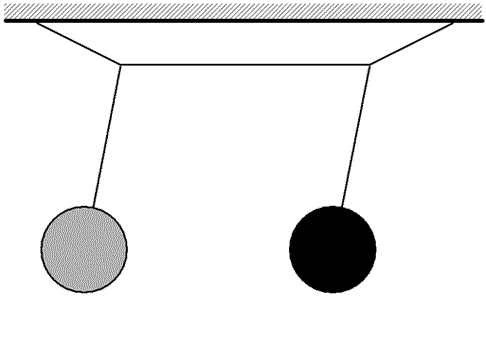
These two pendulums are physically coupled to each other as shown in the sketch. A string is strung like a clothesline and the two pendulums are hung from it. When the gray pendulum swings, it moves the line slightly and pushes slightly on the black pendulum. Now the motion of the gray pendulum is determined by its length, the force of gravity on it, and the force (due to the black pendulum) by the line.
With a plausible model for the force
1) Hold the black pendulum still and start the gray pendulum swinging. As time goes by, the black pendulum is forced into oscillation. The energy added to the black pendulum is extracted from the gray pendulum, which dies down, and eventually comes to rest. Now the black pendulum drives the gray one, and the energy begins to oscillate back and forth between the two pendulums.
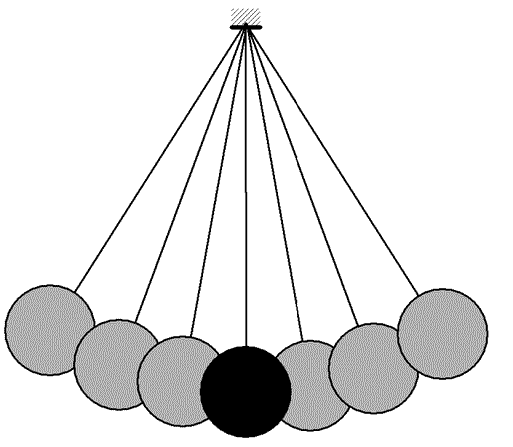
2) Pull both pendulums to the left and release simultaneously. Now the pendulums swing as one, with no variations, with
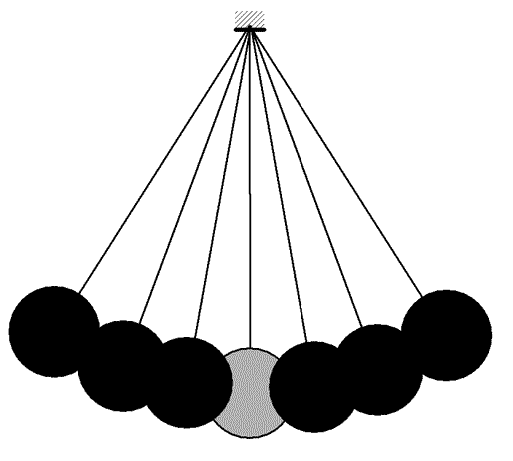
3) Pull one pendulum to the left, and one to the right, and release simultaneously. Once again, the pendulums swing with no variations. Now the period is determined by the length of the pendulum strings and also by the strength of the coupling between pendulums. This period is shorter than the period above because the restoring force is larger.
In the equations below, theta represents the angle that one pendulum makes with the vertical. For the coupled pendulums, theta GRAY is not independent of theta black. The coupling is exposed by experiment 1 above. Experiments 2 and 3 above show that there is a pair of independent variables to describe the behavior. Those two variables are named Phi S and Phi A in the equation below.
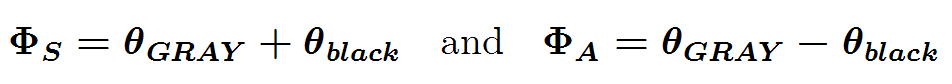
Phi S is important when the two pendulums swing together, as in experiment 2 above, and this motion has a somewhat longer period than the period for Phi A motion (important when the two pendulums are "opposite," one being positive when the other is negative. In terms of the two independent variables, we can represent the original variables in terms of these independent variables, using
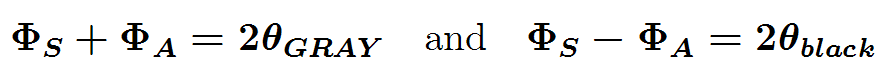
In the new variables, experiment 1 involved a mix of the two variables. Since the two new variables have two different frequencies of oscillation, sometimes they add (both positive at the same time) and sometimes they subtract (one positive when the other is negative). This means that sometimes the gray bob oscillates and sometimes the black one does. The shift between gray and black oscillation can be regarded as a beat between oscillations in the two independent variables, Phi S and Phi A . Once these independent variables are identified, the description of the physics is simplified.
For a more ordinary example, consider the worker pulling a box with a rope, as sketched. The box is moving to the right in the drawing.
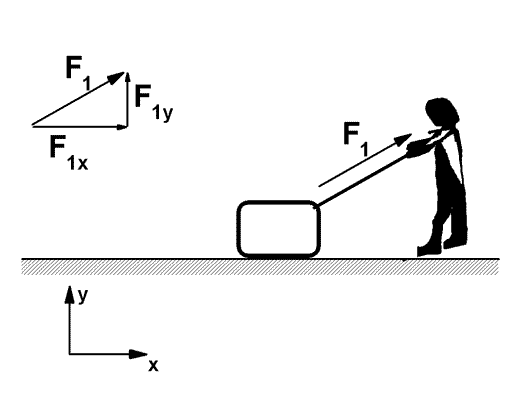
The x and y components of the force by the rope on the box F1x and F1y, are independent of each other; their relation can be changed by changing the angle at which the rope pulls.
The force of gravity has a negative y component, and the x component of the force of gravity is zero, no matter what
The y component of the force by the floor is "whatever it takes" to make the net force in the
The floor has friction. The x component of the force by the floor is called the "friction" force, and it acts in the direction opposite to the direction of the velocity of the box. (The direction of the friction force and the direction of the velocity are not independent; they are coupled.)
In the simplest models for the friction force, the size of the sliding friction force is determined by the size of the normal force. The simple formula tells us to find the friction force magnitude as the product of the normal force magnitude and the "coefficient of friction."
That is, the x
A more exotic example of coupled variables is the Foucault Pendulum. Like the box on the floor, the coupling results from a constraint on the motion of the object. In this case, the pendulum is constrained to move on the rotating surface of a spherical earth. The motion of the pendulum back and
-
Contact Information
Contact Number: 717-871-4297
Email: physics@millersville.edu