Experiment of The Month

We may calculate the rate of precession of the plane of oscillation of a Foucault pendulum by considering a simple case; A ball launched to the north. We ignore the vertical component of the motion and focus on the component of motion in the plane tangent to the earth's surface. We consider the case in which the velocity is constant.

(For a complete description, we must also account for the motion of a ball traveling to the east. This turns out to take a little more work. A geometric derivation of the rotation for both directions is given here. Thanks to Hugh Rance for stimulating this version.)

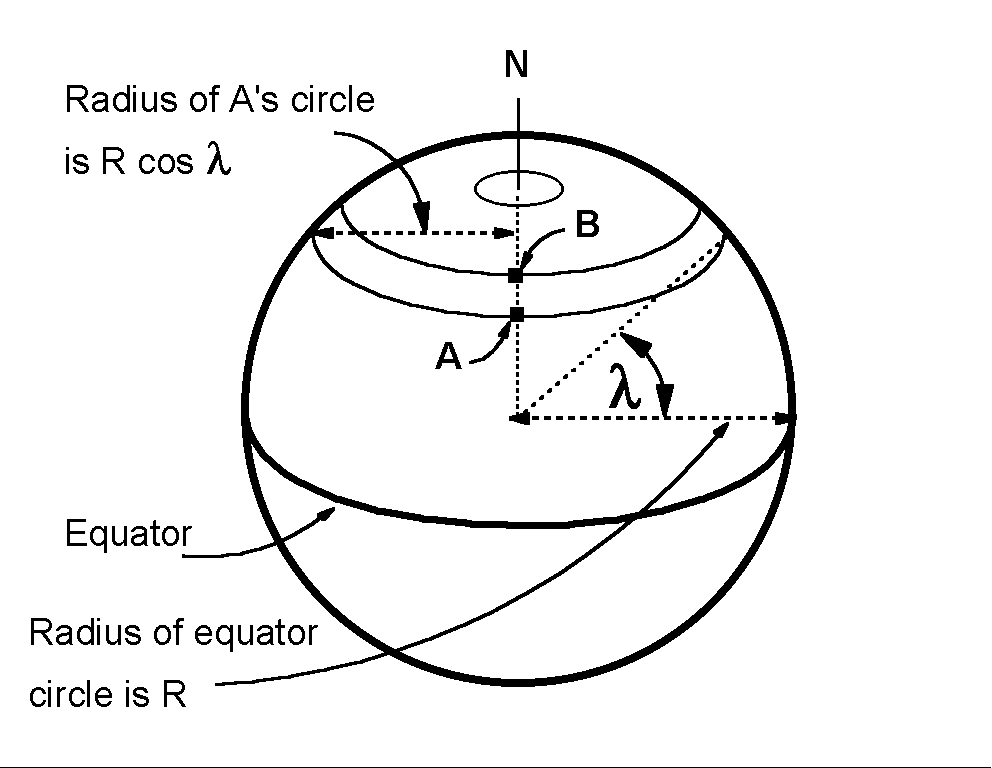
The situation is sketched on a globe in the figure at the right. The ball is launched from point A, towards point B which is (and which remains) due north of A. The angle lambda is the latitude of point A. As time goes by and the earth rotates to the east on its axis, both A and B will move to the right in the figure.

Because both A and B make one revolution each day, and because A moves on a larger circle than B, the velocity of point A is larger in magnitude than the velocity of point B.

The figure at the right shows the ball velocity components: The northward velocity (V_"NORTH")and the velocity (V_A)that it has because it began at rest with respect to point A. The figure also shows the position of A and B (as open squares) at a special later time. At this later time, the ball has reached the latitude of B.

In their new locations, B is still to the north of A.

Because the ball's original "NORTH" velocity component has not changed, and because V_A is greater in magnitude than V_B, the ball arrives to the east of location B.

This shift is the basis of the Foucault rotation. The line from the ball back to A is no longer the same as a north-south line. We will calculate the angle between this line and the north-south line.

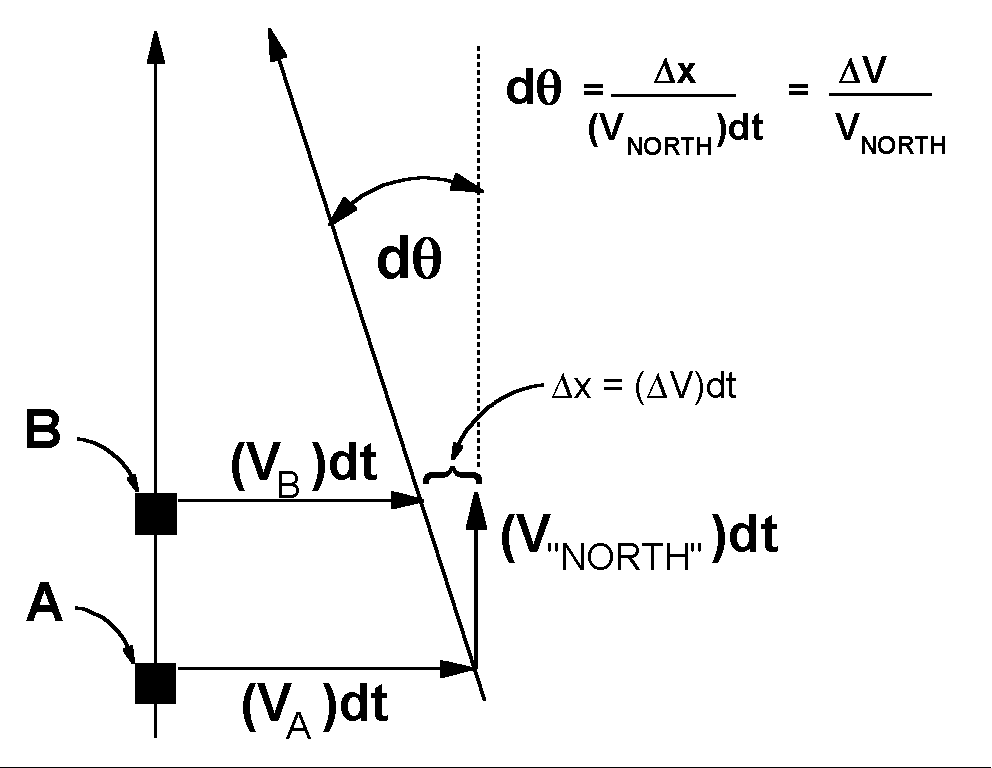To keep things simple, we take the velocities V_A and V_B to be perpendicular to V_"NORTH". This is a safe approximation of the distances travelled are small enough. to represent this smallness, we represent the time of travel of the ball by the time differential, dt.

The shift between the ball's position and B's new position is determined by dt and the difference between the two velocities_A and V_B , as shown in the figure. The angle (dtheta) in radians is the ratio of that difference to the northward distance, (V_"NORTH")dt , that the ball traveled.

It turns out that we can calculate this ratio in terms of the latitude of points A and B. To do this, consider the next figure:

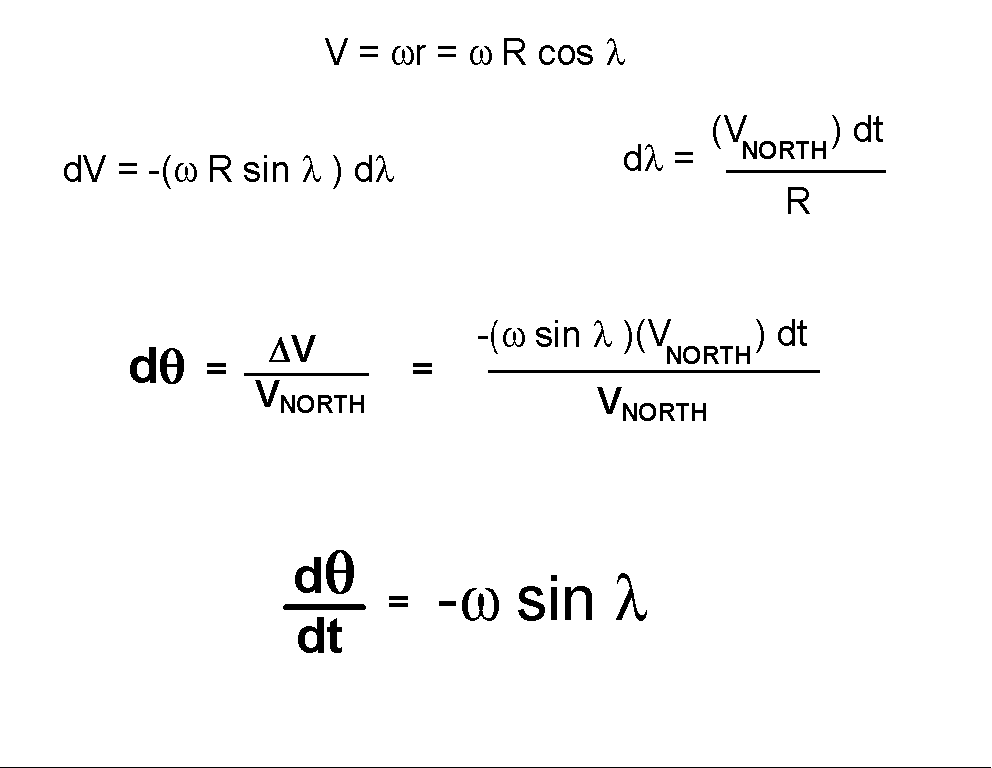The tangential velocity at A is just the angular velocity of the earth, multiplied by the radius of the circle on which A moves. As shown, this can be written in terms of the radius of the earth and the latitude. (See the top figure for reference.)

We use differentials to calculate the difference in velocity between the (nearby) points A and B. We note that the differential change in latitude is caused by the ball's north velocity, and may be calculated in terms of the northward displacement of the ball . Plugging all this in we have the simple final expression for dtheta and the rate of change of direction of travel of the ball, (dtheta)/dt.

The result does not depend on the size of the ball's northerly velocity. Thus it is not sensitive to changes in the ball's velocity. This means that the result transfers directly to the motion of the pendulum bob, even though the bob is not moving at constant velocity. If the earth rotates counterclockwise, the plane of oscillation will rotate clockwise, at a rate generally slower than one revolution per day. Since Millersville is at about 40 degrees north latitude, the rate of pendulum plane rotation is only about 2/3 of the rate at which the earth rotates.

This rotation amounts to a change in the direction (relative to north) of the velocity of the ball, even when the velocity magnitude of the ball stays constant. In a frame of reference fixed on the earth the ball is seen to be accelerated. This observation is due to the fact that the earth frame of reference is accelerated. The acceleration is said to be caused by a force called the Coriolis force.