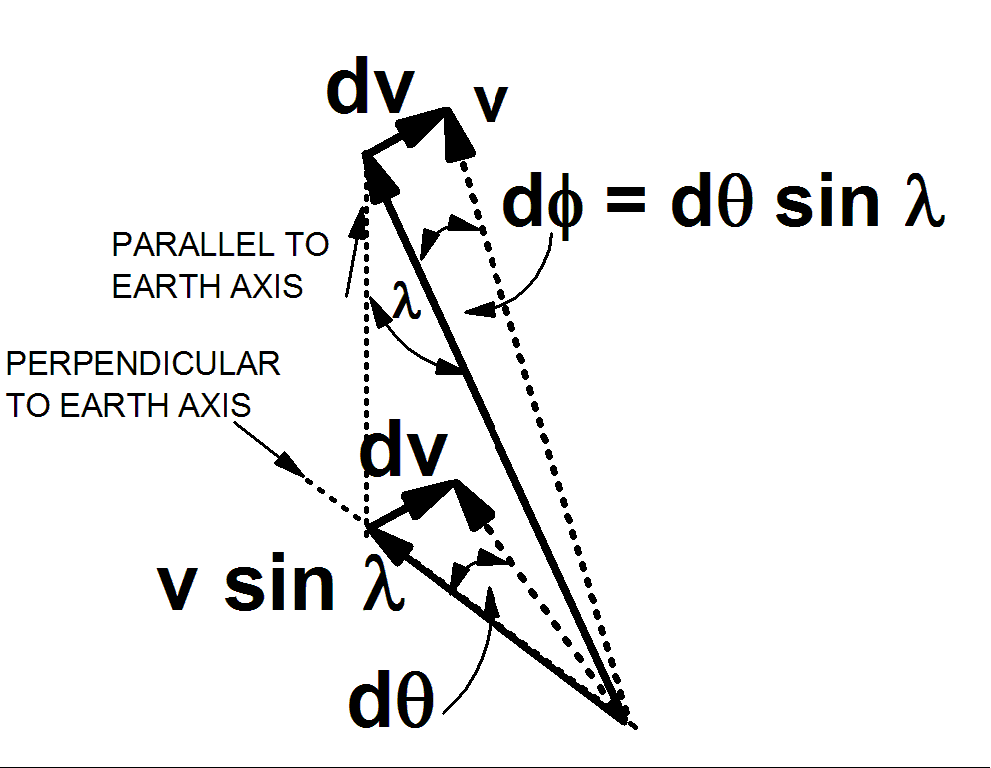Experiment of The Month
A Geometric Derivation for the Rate of Rotation in Foucault's Pendulum
The plane of oscillation of the Foucault pendulum rotates clockwise in the northern hemisphere. At the north pole the plane of oscillation would make one complete rotation during one day. At other latitudes, the rate of rotation is slower. The slower rate is not difficult to derive if the initial motion of the pendulum is north-south. One such derivation is here.
For this month's article, we take a different approach, which is applicable for any initial direction of oscillation. The focus of attention will be a vector v. v can represent the direction of a gyroscope axis, or is can represent the velocity of the pendulum bob. It will probably be easier to think of the gyroscope, because we will allow v to point in any direction, for our convenience.
We will use three different coordinate systems to calculate the components of v:
1) The ordinary north-south, east-west system, with origin at some point on the earth's surface, lying in a plane tangent to the earth at that point.
2) A system with one axis parallel to the earth's axis, and another perpendicular to the earth's axis, going through the point of interest on the earth's surface.
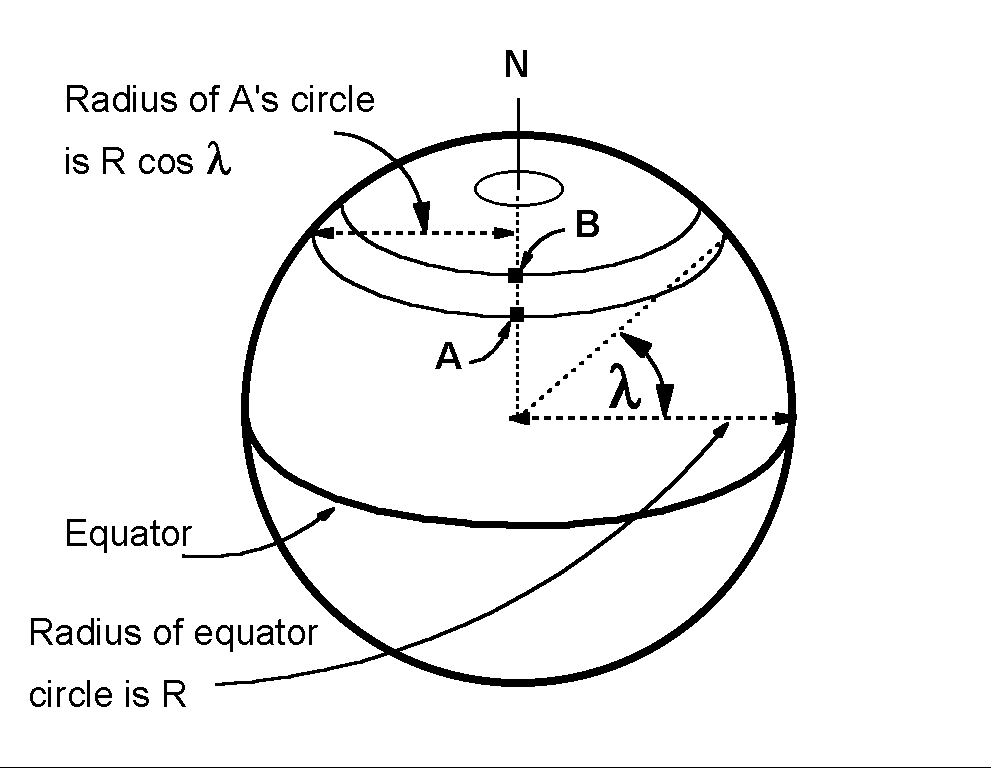
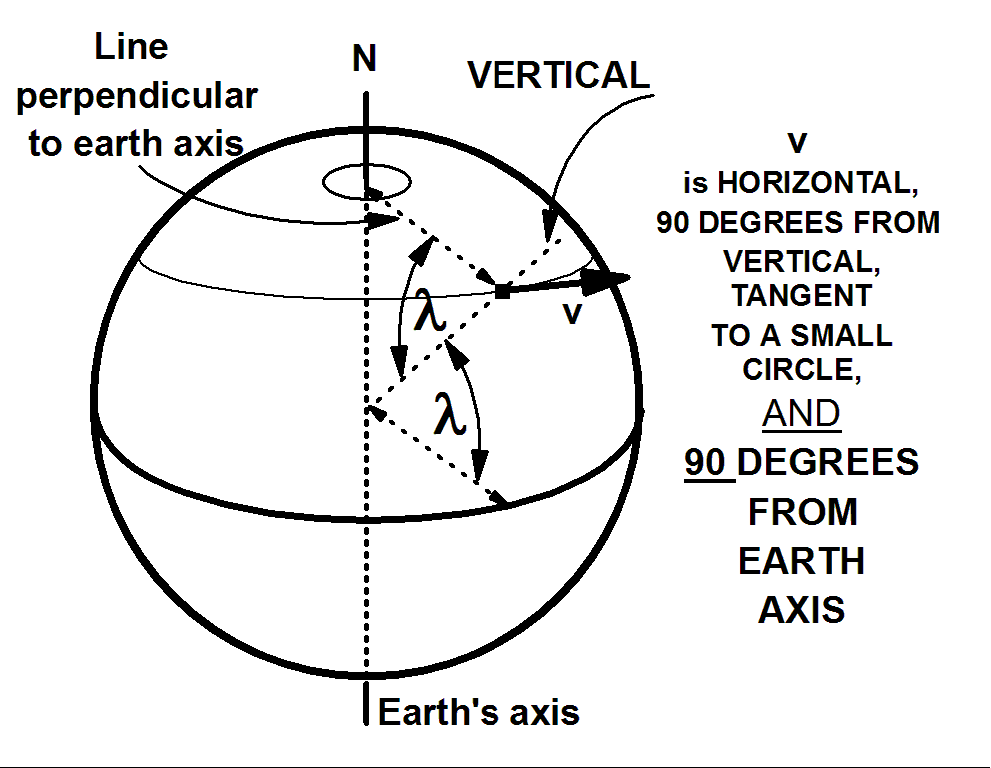
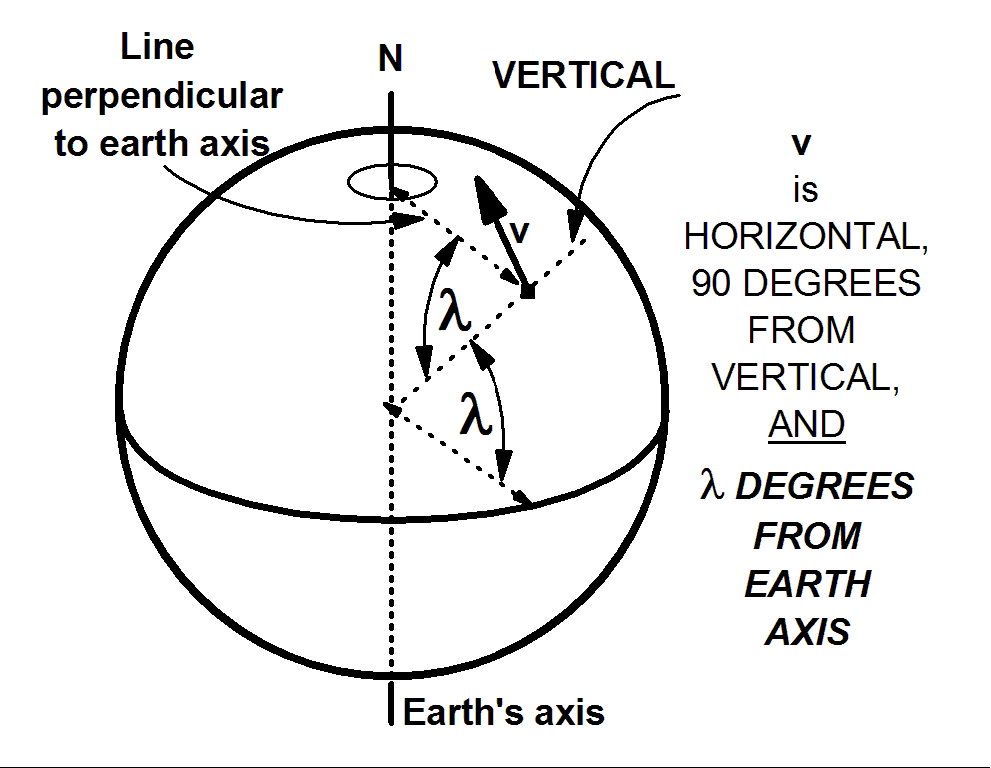
3) An extension of (1) to include the vertical, an axis along the line from the center of the earth to our point of interest. Horizontal vectors are perpendicular to this vertical axis. This line and the earth's axis define a plane. The angle between this vertical axis and a line perpendicular to the earth's axis is the latitude, l, of the point of interest.
We begin by considering two special cases for the direction of v. First, the direction of v is parallel to the earth's axis. This direction is not horizontal, unless we are at the equator. To visualize this direction in the northern hemisphere, lay a ruler on the floor, along the north-south direction. If you are at latitude 50 degrees north, pick up the northern end of the ruler, and raise it until the ruler makes an angle of 50 degrees with the floor. That ruler is now parallel to the earth's axis.
v continues to point along the earth's axis as we rotate with the earth, and we carry the v along with us. (It helps to think of v as indicating the spin axis of a gyroscope.) We detect no change in the direction of this v as the earth rotates.
Second, v is pointed in a direction perpendicular to the earth's axis. If we ignore the tilt of the earth's axis, and the progress of the earth in it's orbit, then we can imagine that v points toward the sun. Now, as the earth rotates, we can tell. At noon, v points more-or-less up, making an angle of l with the local vertical. At midnight, v points more-or-less down, making an angle of l with the local vertical.
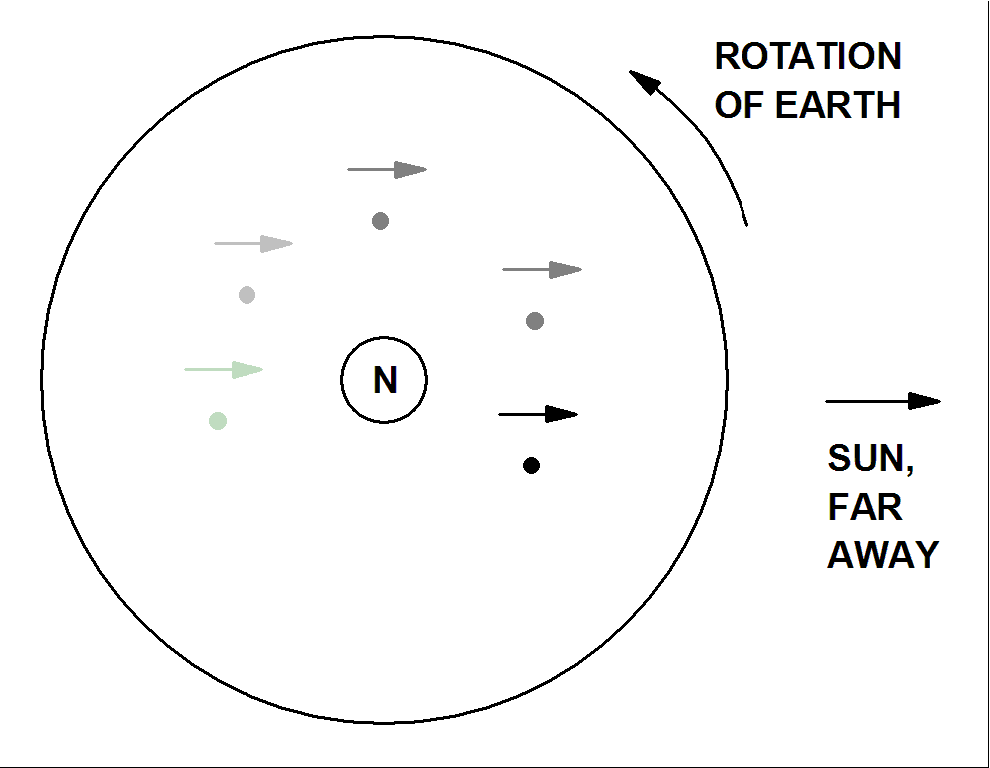
The picture shows a "top" view, looking down on the north pole. The dot represents the tip of the v vector in the first case, pointed along the axis of rotation of the earth. It does not change as it is carried along with the rotating earth.
The arrow towards the distant sun represents v in the second case, pointing always towards the sun. Its direction relative to the earth changes as the earth rotates. Sometimes this arrow points towards the earth's axis (night time in this example). Sometimes it points away from the earth's axis (daytime in this example). It is this arrow that tells us the earth is rotating on its axis. As the earth makes one complete revolution, this arrow makes one complete revolution (relative to the laboratory).
Neither of these arrows is horizontal: Neither lies in a plane tangent to the earth's surface, as they ride a particular location on the earth. To use this picture to understand the Foucault pendulum, we must understand how it connects to horizontal motion.
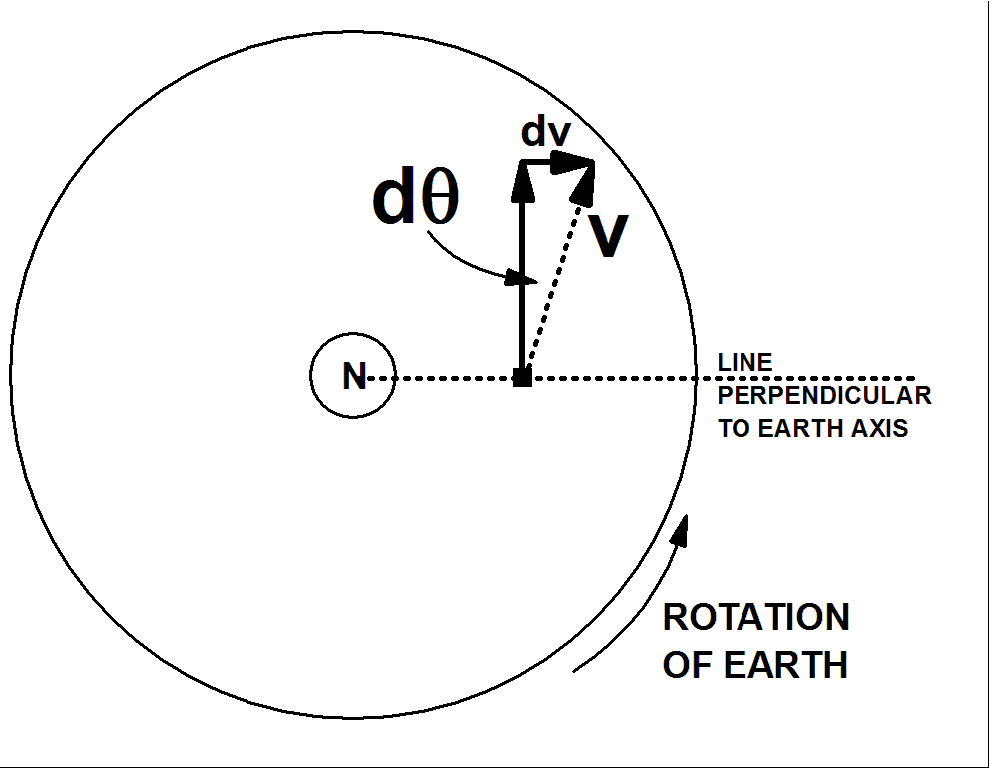
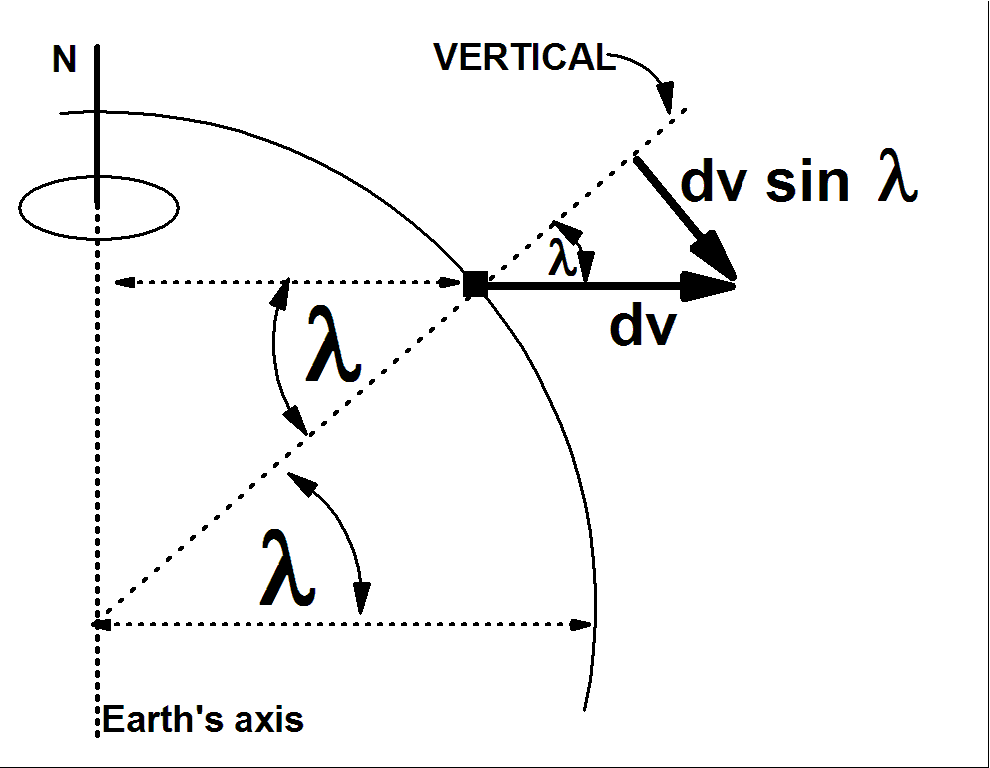
Case 1: v "pointing north," and lying "horizontally" in a plane tangent to the earth. The sketch shows the idea. To follow the effect of the earth turning we consider two components of the vector, v:
1) the component parallel to the earth's axis. This component does not change as the earth rotates.
2) the component perpendicular to the earth's axis. As viewed by someone riding the earth while it turns through a small angle dq counterclockwise, this component turns the same amount, dq, clockwise.
We calculate this perpendicular component using the latitude, l. Since v is perpendicular to the vertical, the angle between v and the line perpendicular to the earth's axis is (p/2 - l). This means that the angle between v and the earth's axis is l, so that the perpendicular component of v is
v sin l
The sketch at the right shows this component in detail. Look first near the bottom of the sketch. The dotted arrow is the observed direction of (vsinl), after the earth has rotated through dq. For small angles (in radians),
dq= (dv)/(v sin l)
where dv is the change in v sin l and also in v, since there is no change in the other component of v (the component parallel to the earth's axis).
That same dv is shown added to the original v vector, near the top of the sketch. The vector v rotates through and angle
df = (dv)/(v) = dq (v sin l)/(v) = dq sin l
This leads immediately to the result that the rotation rate of the pendulum velocity vector is smaller than the rotation rate for the earth by the factor sinl.
Case 2: v "pointing east," and lying "horizontally" in a plane tangent to the earth. The sketches below show the idea.
v lies perpendicular to the plane defined by the earth's axis and the vertical. The line perpendicular to the earth's axis is also in that plane, and is also perpendicular to v. When the earth rotates (counterclockwise) through a small angle dq, an observer riding on the earth sees this vector rotate through exactly the same angle (clockwise). The reason is that in this case, v has no component perpendicular to the earth's axis.
The change in velocity, according to the observer is
dv = v dq
for small angle dq measured in radians.
The direction of this dv vector is along that dotted line which is perpendicular to the earth's axis. To apply the idea to the Foucault pendulum we must account for the fact that the pendulum motion is not allowed to change in the vertical direction. (The tension in the string can change, but to first order, the period is independent of the earth's rotation rate.) The pendulum acts to eliminate the vertical component of dv.
To eliminate dv(VERTICAL), we must take the horizontal component of dv. This is most easily done from a point of view standing just to the west of the pendulum, as in the figure at right. Note that, by definition, horizontal is perpendicular to vertical.
dv(HORIZONTAL)= dv sin l= v dq sin l
When the horizontal component is added to the original v, the new vector makes an angle
df = (dv)/(v) = v dq sin l/(v) = dq sin l
This is exactly the same relation between earth rotation and observed rotation of the vector as for the north-pointing case. For a general horizontal vector, both the north and the east components rotate at the same rate, so that all horizontal vectors rotate at the same rate, for a given latitude, l. The rotation rate is given by
df/dt = (dq/dt) (sin l)
The time for one revolution of the Foucault pendulum at latitude l is given by
(T(PENDULUM) )(sin l) = T(EARTH)
Thanks to Hugh Rance for stimulating this version.
-
Contact Information
Contact Number: 717-871-4297
Email: physics@millersville.edu