Experiment of The Month

The MU Physics Department does not claim to have invented these labs. Actually, the origin of these labs is currently unknown to us. Our labs do not have written instructions. In keeping with this spirit, the description given here will be brief and general. The intent is that each performance of the lab will be unique; in each nature will reveal a slightly different face to the observer.

If wind resistance can be ignored, we assert that a ball thrown through the air obeys a very useful rule as it moves: The vertical component of the motion is independent of the horizontal component. The aim of this exercise is to test that assertion.

In preceding exercises we have measured the acceleration of various falling balls, and found evidence that they have the same, constant, acceleration, directed downwards. In this exercise, we determine the acceleration of a ball thrown up with an initial velocity about 45 degrees above the horizontal. The flight of the ball is videotaped, and the video is analyzed to determine the acceleration.

We use a rolling chalk board, about 3' by 5' as a backdrop for the scene to be video taped. Before taping the flight of the ball, we swing a 1 meter pendulum in front of the board, and tape its motion. The period of a 1 meter long simple pendulum is very close to 2 seconds (2.01 seconds); the same as a pendulum on a grandfather clock. As a test of the data collection process, we use the video tape to determine the time that it takes the pendulum to swing from its left extreme to its right extreme position. This should be 1 second; the same as the time for a "tick" of a grandfather clock.

We use a good quality consumer camcorder, on a tripod, and video capture software and hardware called SmartCap. For the analysis we use the "Videopoint" program from Pasco. Data are taken on a single computer at the front of the room, and transferred over a network to each student pair's lab bench computer. In this year's version of the exercise, all students analyzed the tape of a single ball flight. This saved time, but raises the question of whether the results are reproducible. In previous semesters, each pair of students has made a separate video tape.

The Videopoint soft ware calibrates distance when the student clicks the mouse on first one end, then the other, of the 1 meter pendulum. Students then advance the record, frame by frame, and click the mouse on the picture of the ball in each frame. The software produces a table of the time, and the x and y values of position for each click.

This data table is copied to a spreadsheet (Excel in our case), with separate areas for the x and y components of the motion. Students use spreadsheet arithmetic to calculate the velocity for pairs of points. To avoid the question of whether to assign the time for that velocity to the first or the second point, this strategy is used: We form the pair by skipping a point, (using for example the difference between points number 2 and 4) and assign the velocity to the time for point number 3. This method has the disadvantage of being more removed from instantaneous velocity than the data require.

The Videopoint software actually calculates velocities, and can be optimized. However, the lab instructors prefer to have students create their own analysis when possible.

In the next spreadsheet column, students then use the velocity values to calculate the acceleration, using again the "skip-a-cell" trick. The table below represents the vertical component of the data set used for this semester's exercise. Graphs of position, velocity, and acceleration versus time are shown below, for the y component of the motion.

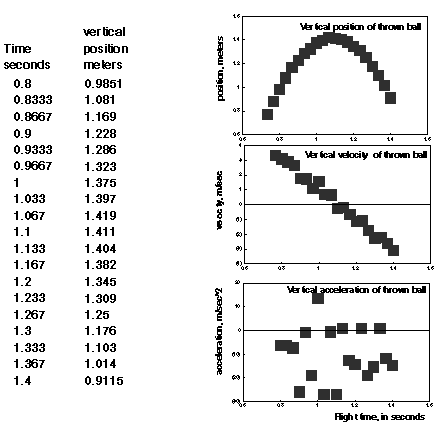
The position curves are fairly smooth, and the velocity curves exhibit clear trends, but the acceleration plot is wildly varying. Small errors in the position measurements are magnified when the second derivative is taken. In a typical analysis from this exercise, the standard deviation of the vertical component acceleration is greater than the average value, so that the vertical acceleration value is consistent with zero.

Yet the graphs of velocity versus time clearly show that the rate of change of velocity is about -10 (m/sec)/sec for the vertical component, and zero or slightly decreasing for the x component (not shown). Students draw by hand a straight line through the velocity points and estimate the slope of the line, from the graph.

Students are meant to take home the particular information that the ball in an arcing trajectory has the same acceleration (about 10 m/sec^2 downward) as the ball falling straight down. They are meant to take home the general message that people, and not machines, are responsible for making sense out of data.