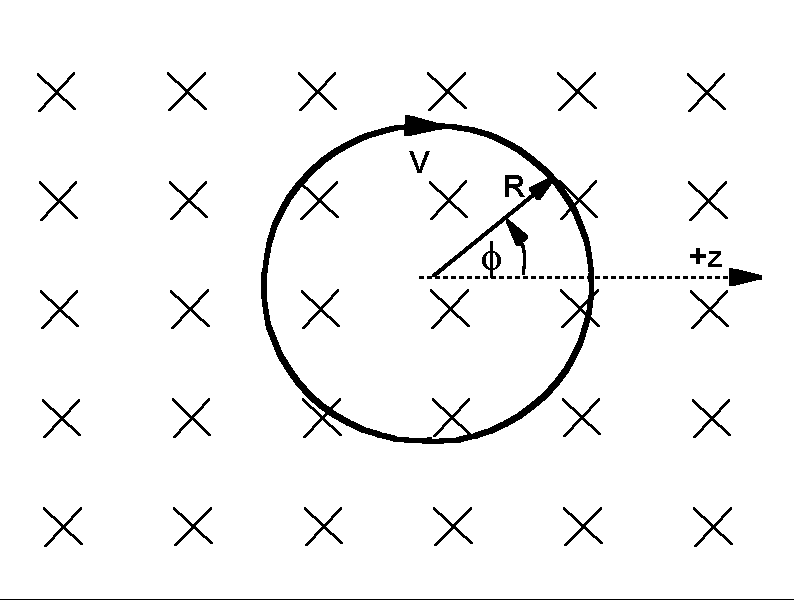Experiment of The Month
A lecture on laboratory realization of a Relativistic Clock
In the fall semester of 1999, Dr. Dieter Forster https://phys.cst.temple.edu/dieter-forster.html spoke to the MU senior physics seminar. Although we have not done the experiments suggested, the talk was so interesting that a segment of it is transcribed for this months offering.
This segment describes a clock made from a charged particle orbiting in a magnetic field. (One trip around the orbit may be regarded as one "tick" of the clock.)
The figure shows an electron orbiting in a uniform magnetic field. The velocity of the electron is always in the plane of the picture, and the magnetic field is perpendicular to that plane, pointing
The electron orbits with the familiar "cyclotron frequency," given 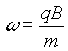
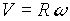
We think of the circular orbit as occurring in the 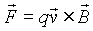
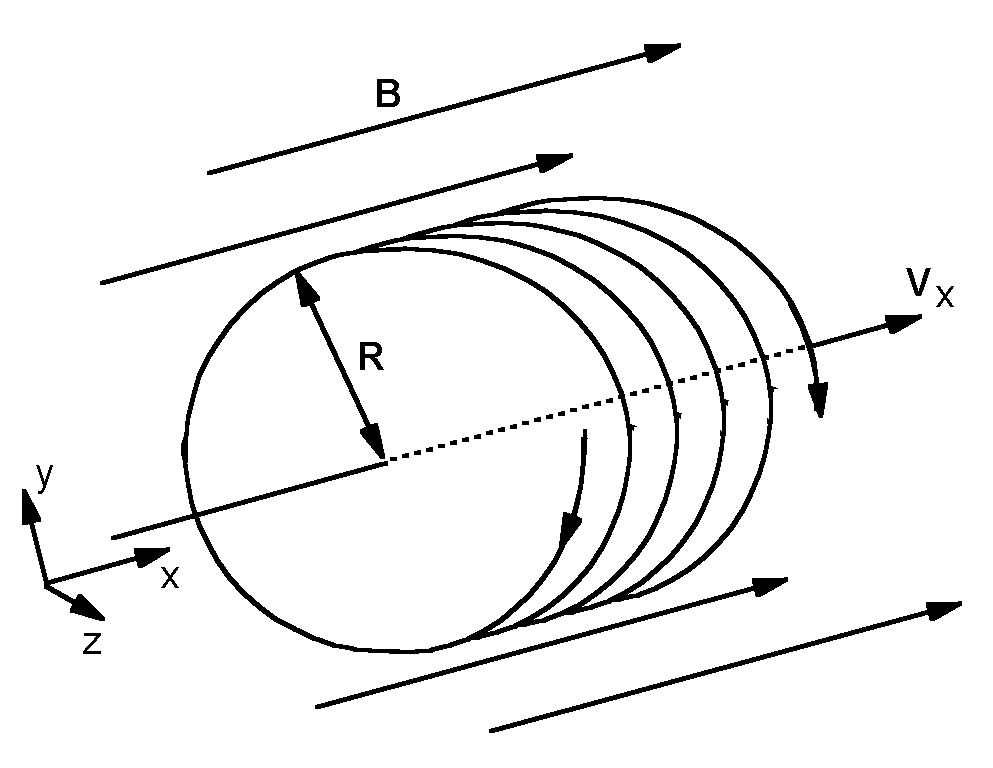
If the particle has a component of velocity in the direction parallel to the magnetic field, that component has no effect on the "cyclotron orbit" in the
Dr. Forster used a mix of Einstein's relativity and classical physics to develop an experimental demonstration of "time dilation." In the
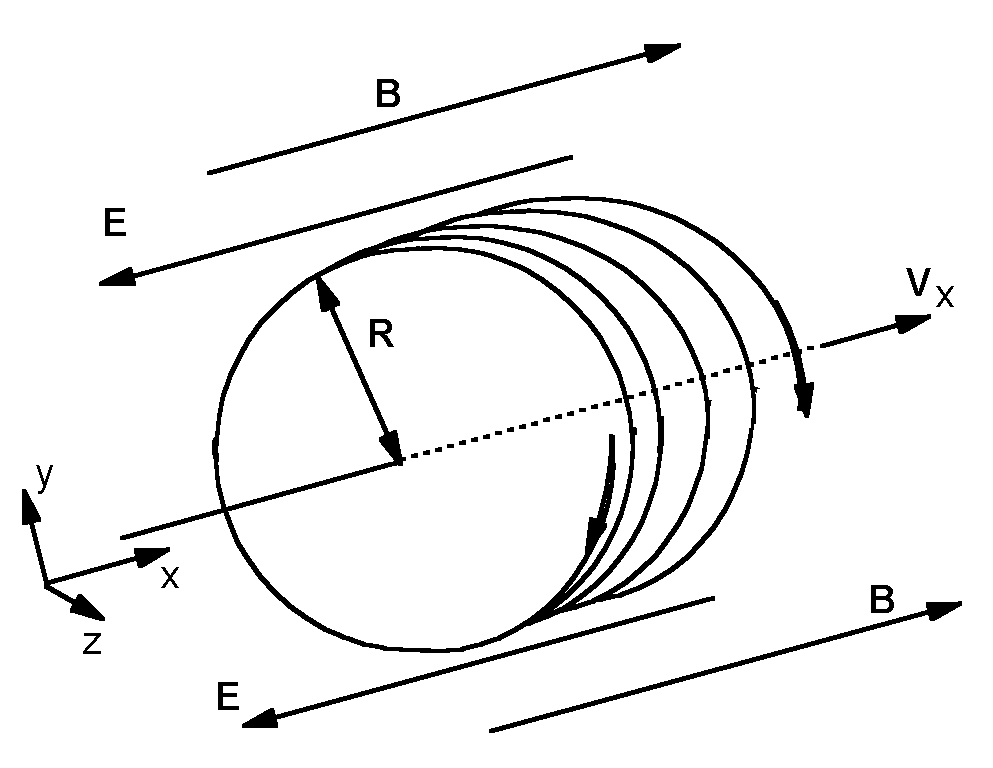
To cause the change in the x component of velocity, an electric field, symbolized by E, is added to the experiment. The electric field accelerates the charge in the +x direction so that the x component of its velocity increases without any change in the motion in the
In the figure, the electric field is represented by arrows. Because the charge in this example is negative, the electric field must point in the -
The Lorentz force is now given 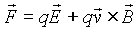
Dr. Forster used these classical forces along with a version of Newton's second law that is corrected to include Einstein's relativity. Recall that Newton wrote his second law (in modern notation) 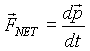
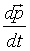
Newton defined the momentum, p, as 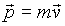 The relativistic momentum is calculated in a slightly different way
The relativistic momentum is calculated in a slightly different way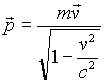
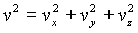
Dr. Forster proposed using the orbit period of the electron in a magnetic field as the clock "tick." He used the relativistic momentum and the (otherwise) ordinary Newton's second law with the ordinary electric and magnetic forces to predict the behavior of the
The clock electron orbits in the
Along the 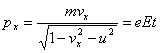
In this equation, 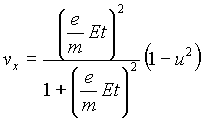
For the
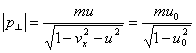 where u0 is the initial value of the tangential velocity, and the initial value of the x component of the velocity is taken to be zero.
where u0 is the initial value of the tangential velocity, and the initial value of the x component of the velocity is taken to be zero.
The momentum direction, however, does change. The rate of change of momentum is equal to the magnetic force. The z component of Newton's second law is
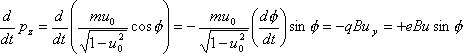
Using the relation of u to the x component of v, this can be solved for the angular velocity in the
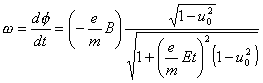 .
.
The period of the orbit is given by
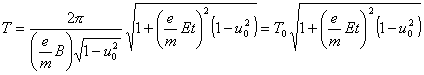 ,
,
and if this is written in terms of the x component of velocity, the clock period is (for small orbital velocity)
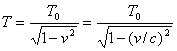 .
.
This is the usual "time dilation," now appearing in a reasonably realistic moving clock. In the last part of the expression, we have converted back to mks units, so that the speed of light appears explicitly.