Experiment of The Month
Inertial and Gravitational Mass
Again and again in beginning physics problems using the force of gravity, the masses on both sides of 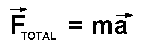 cancel. A bicycle going down hill reaches the same speed at the bottom, no matter what mass it carries. Einstein elevated this observation to a postulate: The inertial mass (which appears on the "ma" side) is identical to the gravitational mass (which appears on the "force" side).
cancel. A bicycle going down hill reaches the same speed at the bottom, no matter what mass it carries. Einstein elevated this observation to a postulate: The inertial mass (which appears on the "ma" side) is identical to the gravitational mass (which appears on the "force" side).
The assertion that inertial mass and gravitational mass are identical is called the "equivalence principle." This exercise demonstrates the idea. We measure the mass of a rubber stopper in two different ways. One way measures the inertial mass and the other way measures the gravitational mass.
(A sensitive test of the equivalence principle is based on a different prediction: that the period of a pendulum is independent of the mass of the pendulum. This month's experiment is best regarded as a demonstration of the meaning of equivalence, rather than a test of the principle.)
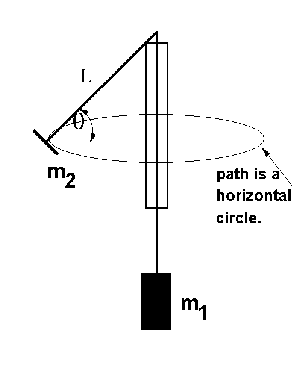
In the experiment, a rubber stopper is spun in a horizontal circle, as shown in the photograph above. The thread spinning the stopper runs through a glass tube (such as a pipette tube) with a smooth polished rim. On the other end of the thread, a 50 gm mass hanger supplies the tension in the thread.
It takes some practice to keep the stopper spinning with only the hanger touching the thread. It is easy to let the hand "lean" against the thread as it comes out of the bottom of the tube. This keeps the stopper spinning nicely, but makes analysis impossible.
Dr. Miziumski has the nicest way to analyze this motion; nicest because it does not require knowledge of the angle, theta. The result is 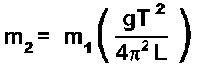 where T is the period, and L is the length of the string measured from the top of the tube to the center of the stopper. T is determined by measuring the time for 10 periods and dividing by 10. The usual mistake in this part is to count starting at 1 when the stopwatch is started, and to stop the watch on the count of 10, giving the time for 9 periods.
where T is the period, and L is the length of the string measured from the top of the tube to the center of the stopper. T is determined by measuring the time for 10 periods and dividing by 10. The usual mistake in this part is to count starting at 1 when the stopwatch is started, and to stop the watch on the count of 10, giving the time for 9 periods.
The mass, m2 of the stopper, measured in this way, is the inertial mass. It is compared to the gravitational mass of the stopper, using a top loading balance. Of course the two numbers are not equal; the question is whether they agree within experimental error.
We use this lab as an opportunity to propagate error, using the standard deviation of 12 measurements of period, and a personal estimate of the uncertainty in the length L, during the progress of the experiment. (We mark the string with ink to help keep L constant.)