Experiment of The Month

If people remember the "force table" from their introductory physics laboratory experience, it is usually an unpleasant memory. It seemed contrived, overly complicated, and did not work very well.

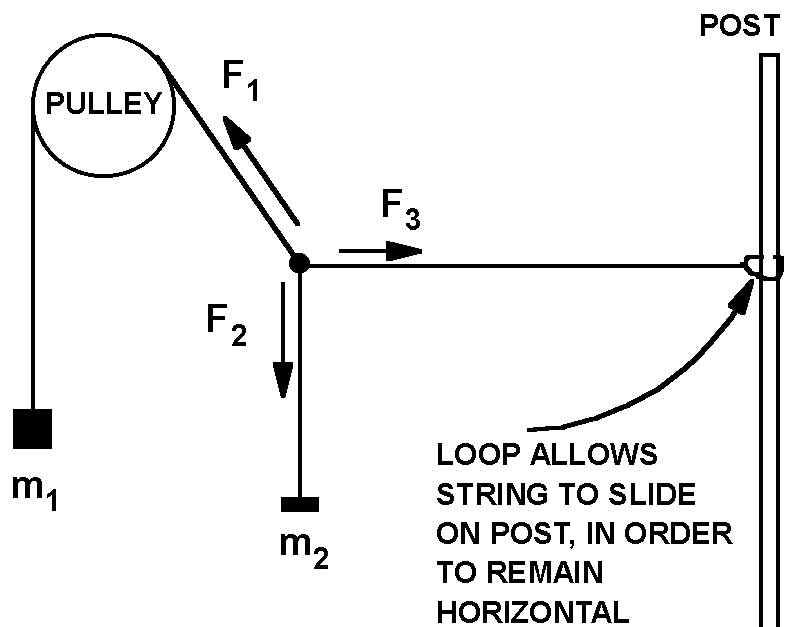
Dr. Cooney developed a simpler version that lends itself to the kind of individual variations that our professors like to try as they teach their individual laboratories. It consists of a long string that drapes one end over a pulley and the other end has a loop that wraps around a vertical post, as shown in the sketch. To this string is knotted a second short string.

Weights are hung on the short string, and on the free end of the long string. The loop on the post is then adjusted up or down until the string segment running from post to knot is horizontal. This trick simplifies the analysis and clarifies the idea of force components.

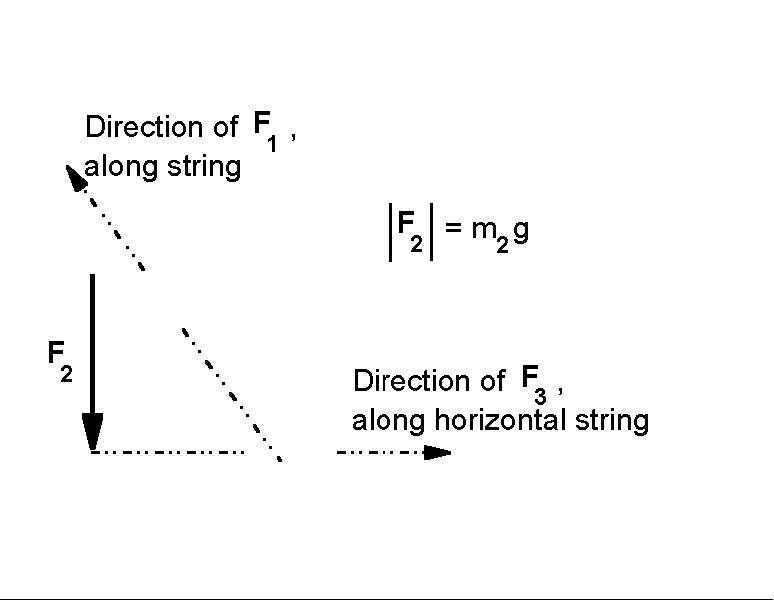
Since the short string is vertical, so that the sum of the horizontal components of the forces labeled F₁ and F₃ must add to zero. These forces are not measured.

Since F₃ is horizontal, the sum of the vertical components of forces F₁ and F₂ must be zero. For given masses m₁ and m₂ , we use a protractor for two purposes:

1. To ensure that F₃ is horizontal, by sliding the loop until its string makes an angle of 90 degrees with the short (vertical) string that attaches to m₂ .
2. To measure the angle between F₁ and the horizontal (having already ensured that the looped string is horizontal).

We repeat this for several combinations of masses, m₁ and m₂ . We ask if one mass must be greater than the other if we must be able to make the looped string horizontal. We ask if it is possible to have the looped string horizontal if m₁= m₂ .

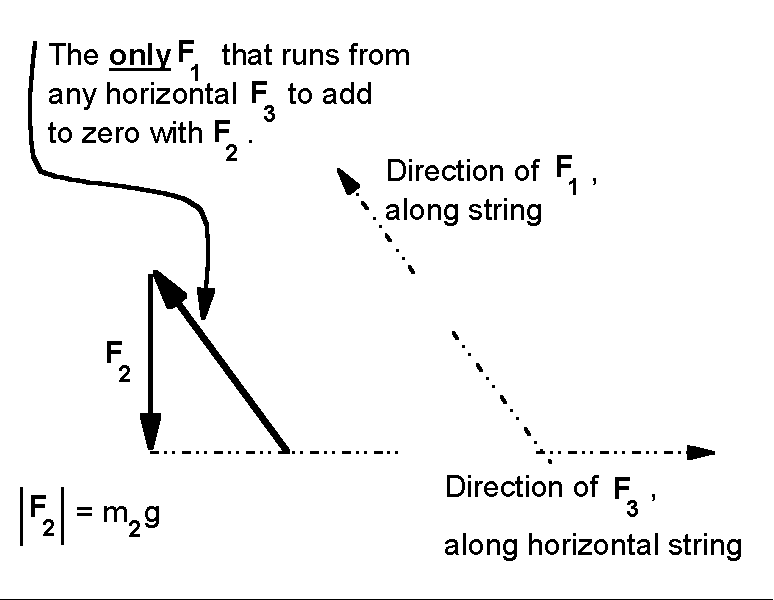
At this point our approaches diverge. Sometimes we plot graphs to display the relation between the angle and the ratio of the masses. Sometimes we plot the vertical component of F₁ versus m₂g . In all cases we aim for an intuitive feel of how forces add, and the beginnings of intuition for the components of a force. For vector sum intuition, the vector sum can be done on paper, using the measured angle to draw the only F₁ that can make the vector sum of forces equal to zero. The ratio of the lengths of the F₂ and the F₁ arrows is equal to the ratios of the masses m₁ and m₂.