Experiment of The Month
The Underwater Pendulum
Senior physics major Robert Lee has a first; a second entry in the Experiment of the Month. For his senior seminar project (as well as his University Honors Thesis and his Physics Department Honors project), he studied a pendulum swinging under water.
In particular, he compared the period of a pendulum swinging under water to the period of the same pendulum swinging in air. His pendulum had a spherical brass bob on the end of a light thread. He made measurements for thread lengths of 22.2cm, 27.4cm, and 29cm.
In each case the underwater period was longer, by about 10% . Textbook treatments of the pendulum might lead one to expect that the period was lengthened because of the "damping force" due to the viscosity of the water. It turns out that damping effects are significantly smaller than two other effects: The buoyancy of the water, and the inertia of the water which the bob must push aside as it swings.
The buoyancy effect was relatively easy for Mr. Lee to calculate. The inertial effect required a more impressive mathematical effort. In the end, his calculations agreed with the experimental measurements within the .005 second uncertainty in the period measurement.
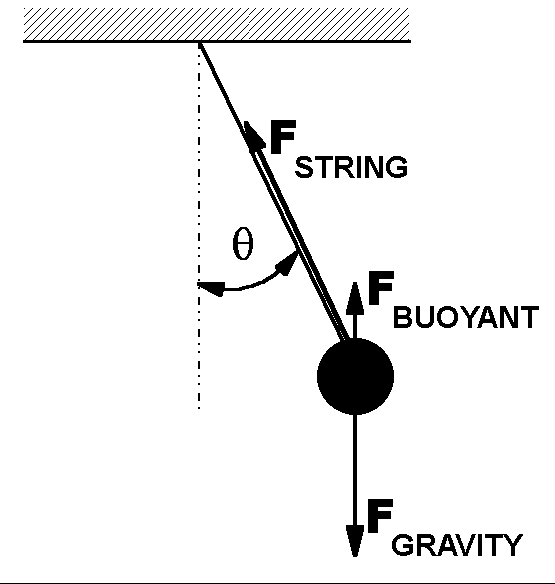
The buoyant force adds a term to the equation relating torque, t, to angular acceleration, a,
tTOTAL=I a
where I is the moment of inertia, and
tTOTAL=-mgLsinq + m(rWATER / rBRASS )gLsinq
where L is the length of the string and the second term on the right is the torque contribution due to the buoyant force. The effect of the buoyant force is to produce (mathematically) an effective gravitational field strength,
g* = (1-rWATER / rBRASS )g
Using this effective g to calculate the period from the usual formula, T2=4p2L/g* accounts for about 2/3 of the shift in pendulum period from air to underwater. Beginning students may want to skip to the end from this point.
To account for the effect of the water flowing around the brass bob, Mr. Lee use a reference frame fixed on the bob, and considered the flow of water past it, when the water far from the bob was moving past at a velocity v. (In the laboratory frame, v is the velocity of the bob through the water.)
He derived an expression for the velocity throughout the fluid, assuming that it was incompressible, irrotational, and (near the bob) was parallel to the surface of the bob. He then calculated the kinetic energy of a unit volume of water, and integrated that kinetic energy over all space.
With this result, he had an expression for the kinetic energy of the water for each value, v, of the bob's velocity. The total kinetic energy of the whole system is then the kinetic energy of the bob, plus the kinetic energy of the water flowing around it. Since the water kinetic energy is known in terms of the bob velocity, the kinetic energy of the system can be written in terms of the bob velocity, v, and an effective inertial mass, m* in place of the bob mass, in the expression
KE = ½ m* v2.
Mr. Lee's calculation gave the water contribution to the effective inertial mass as exactly 1/2 of the mass of water displaced by the bob. This means that the effective inertial mass of the bob is given by
m* = m[1 + ½ (rWATER / rBRASS )]
where m is the "bare" mass of the bob. The effective inertial mass appears in the I term of
tTOTAL=I a
but not on the left side of that equation, because the gravitational force on the bob is not affected by the water which the bob drags along with it.
When I=mL2 becomes I=m*L2 , the more general expression for the period of a pendulum must be used,
T2=4p2I/(mg*L) = 4p2(m*L2)/(mg*L) = 4p2(m*L)/(mg*)
A summary of his results is shown below.
| length, L | measured period in air | measured period in water | calculated period with buoyancy | calculated period with buoyancy and fluid dynamics |
| .222 m | 0.948±.004 sec | 1.039±.005 sec | 1.03 sec | 1.042 sec |
| .274 m | 1.059±.004 sec | 1.160±.006 sec | 1.15 sec | 1.164 sec |
| .290 m | 1.084±.004 sec | 1.184±.005 sec | 1.18 sec | 1.185 sec |