Experiment of The Month
Mass and Newton's Third Law of Motion
 Newton's third law of motion states that when two objects, A and B interact, the force by A upon B is equal and opposite to the force by B upon A. Newton's first law of motion tells us that an object will not spontaneously change its velocity; objects must be forced to change velocity. This experiment concerns these two laws in combination: We study the change in velocities that occur when two objects interact. The components of the experiment range from high technology to low, including air tracks, army surplus nylon thread, computers, video cameras, and flame throwers.
Newton's third law of motion states that when two objects, A and B interact, the force by A upon B is equal and opposite to the force by B upon A. Newton's first law of motion tells us that an object will not spontaneously change its velocity; objects must be forced to change velocity. This experiment concerns these two laws in combination: We study the change in velocities that occur when two objects interact. The components of the experiment range from high technology to low, including air tracks, army surplus nylon thread, computers, video cameras, and flame throwers.
The first part of the experiment begins with two identical air track gliders (the 20 cm size) held together, with springs in contact and compressed, by a loop of thread. The thread is burned with a "flame thrower" (a fireplace lighter) as a means of creating an unbiased release. The springs push apart, obeying Newton's third law. We observe the final velocities of the gliders, after the gliders are no longer in contact. To no one's surprise, the velocities are the same, but in opposite directions.
We use video recorders and software called VideoPoint to capture and analyze data for position as a function of time. We then use Excel software to plot position as a function of time for each glider, and calculate the slope to determine velocity. We could simply use a pair of stop watches to measure the time of arrival of each glider at its end of the air track, but we do enjoy the fancy toys. In later exercises we use the same equipment to collect data on simple harmonic motion, which proceeds to quickly for measurement by hand.
We had hoped to be able to measure velocities during the acceleration phase of the motion, while the springs were still pushing apart. With current apparatus, only 1 or two positions may be measured before the carts have separated. To make statements about the acceleration phase, we must make inferences from the data available.
Each laboratory group reports different velocity magnitudes, because, inevitably, each group compresses its springs by different amounts. The groups consistently report velocities of (nearly) equal magnitude but opposite direction. We infer from this collective information that at each instant during the acceleration phase, the velocities were equal and opposite.
Since the velocity at an instant is the accumulation (sum) of all the velocity changes since the start of the experiment, we infer that each velocity change for one glider was matched by an equal (but oppositely directed) velocity change of the other glider. Since acceleration is the rate of change of velocity, we conclude that at each instant the acceleration of one glider was equal (but oppositely directed) to the acceleration of the other glider.
Comparing this result to Newton's third law of motion, we are led to ask, "Can we use the acceleration of the glider as a measure of the force on it?" The answer is, "No, mostly."
We extend the experiments by adding a second glider to one side of the experiment. On the left is now a single glider (named A), and on the right is a pair of gliders held together with a paper clip. The two-glider object is named B. The clipped-together gliders have stiff springs on them, so that internal vibration is not a problem. The single glider has a soft spring for better control during compression.
When the thread is burned away, the double-glider (B) moves away with a velocity that is (nearly) half of the velocity of the single glider (A). We conclude that the acceleration of the double-glider was half of the acceleration of the single glider. At this point we choose to retain the third law, which asserts that in all cases the forces between the two objects (the single glider and the doubled glider) are equal and opposite.
The quantity which does remain the same (in magnitude) for the two objects is the product of (number of gliders in the object) multiplied by (the acceleration of the object). After testing this relationship for 2, 3, and 4-glider objects, we decide to use the product
(number of gliders in object)X(acceleration of object)
as our measure of force on the object. This measure of force arises from experiment, and is consistent with Newton's third law of motion.
<
To describe the number of gliders we reach back to an old meaning of the word "mass." To "mass" an army is to bring together a number of soldiers. One amasses a fortune in coins. the size of the fortune is the number of coins. We call the number of gliders in our object the "mass" of the object.
If we were able to repeat the experiment with a different object pushing on the single glider, A, we could assign a mass number to the new object in this way: Measure the ratio (final velocity of the new object) divided by (final velocity of the single glider). Determine how many gliders it would take to make a B object with that ratio of velocities. That equivalent number of gliders is the mass of the new object.
The world uses a kilogram object rather than a glider as its standard of mass. However, this experiment helps to make clear how mass measures the amount of material in an object.
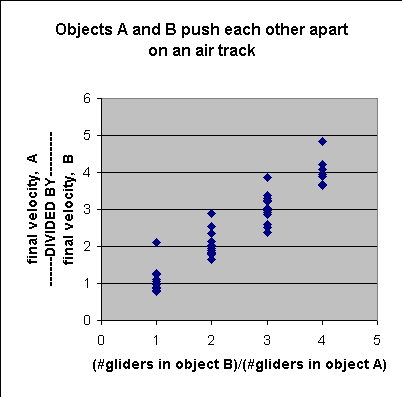
Class results for this experiment are shown in the graph. In the graph, the ratio of velocity magnitudes is plotted versus the ratio of the number of carts. If mass times acceleration is a good measure of force, and if Newton's third law holds, then the slope of the best line through the data should be 1. The slope is 0.99 with an uncertainty of 0.05 . The intercept is 0.06 with an uncertainty of 0.13 .
One set of raw data for the experiments is shown below, for those who might wish to try the calculation for themselves. Listed are the positions of representative points, one point on each glider, as the position of the glider changes with time.
| 1glider | 1glider | 2gliders | 1glider | 3gliders | 1glider | |||||
| Point S1 | Point S2 | Point S1 | Point S2 | Point S1 | Point S2 | |||||
| time | x-pos | x-pos | time | x-pos | x-pos | time | x-pos | x-pos | ||
| [s] | [m] | [m] | [s] | [m] | [m] | [s] | [m] | [m] | ||
| 0 | 0.6882 | 0.64 | 0 | 0.5871 | 0.5418 | 0 | 0.4571 | 0.4181 | ||
| 0.1 | 0.6928 | 0.6423 | 0.06667 | 0.5871 | 0.5418 | 0.06667 | 0.4593 | 0.4181 | ||
| 0.2 | 0.6882 | 0.6423 | 0.1333 | 0.5871 | 0.5395 | 0.1333 | 0.4593 | 0.4138 | ||
| 0.3 | 0.6882 | 0.64 | 0.2 | 0.5916 | 0.5304 | 0.2 | 0.4636 | 0.4051 | ||
| 0.4 | 0.6974 | 0.6354 | 0.2667 | 0.5939 | 0.5282 | 0.2667 | 0.4636 | 0.3986 | ||
| 0.5 | 0.7042 | 0.6263 | 0.3333 | 0.5984 | 0.5214 | 0.3333 | 0.468 | 0.39 | ||
| 0.6 | 0.7134 | 0.6171 | 0.4 | 0.5984 | 0.5123 | 0.4 | 0.468 | 0.3835 | ||
| 0.7 | 0.7203 | 0.6102 | 0.4667 | 0.603 | 0.5032 | 0.4667 | 0.4723 | 0.3791 | ||
| 0.8 | 0.7295 | 0.6033 | 0.5333 | 0.6098 | 0.4987 | 0.5333 | 0.4745 | 0.3661 | ||
| 0.9 | 0.7364 | 0.5941 | 0.6 | 0.612 | 0.4919 | 0.6 | 0.4766 | 0.3618 | ||
| 1 | 0.7478 | 0.5873 | 0.6667 | 0.612 | 0.4851 | 0.6667 | 0.4788 | 0.3531 | ||
| 0.7333 | 0.6166 | 0.4828 | 0.7333 | 0.4831 | 0.3445 | |||||
| 0.8 | 0.6256 | 0.4715 | 0.8 | 0.4853 | 0.3401 | |||||
| 0.8667 | 0.6256 | 0.4647 | 0.8667 | 0.4875 | 0.3293 | |||||
| 0.9333 | 0.6279 | 0.4579 | 0.9333 | 0.4918 | 0.3206 | |||||
| 1 | 0.6302 | 0.4534 | 1 | 0.494 | 0.3141 | |||||