Experiment of The Month
Demonstration of Anomalous Dispersion
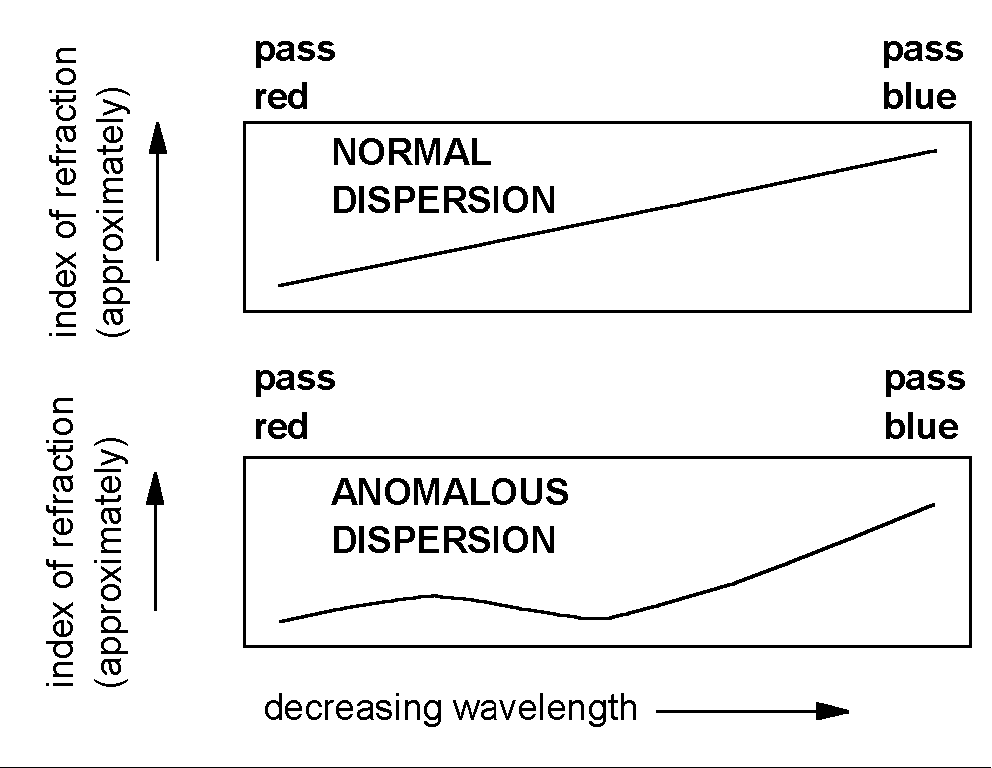
When a beam of white light is refracted by an ordinary prism it is not only redirected; it is also dispersed. This dispersion occurs because the index of refraction depends (slightly) on the wavelength of light being refracted. In most materials, blue light is refracted more strongly than red light. Blue light is bent at a larger angle than red by a normal prism. Normal dispersion produces the familiar rainbow of colors from white light.
Normal dispersion is understood to arise because the atoms in the prism are capable of oscillating at natural resonant frequencies which are much higher than the frequency of visible light. Light with higher frequency (shorter wavelength) interacts more strongly with these atoms because it is closer to the resonant frequency. As a result it is slowed down more by its interaction, and has a larger index of refraction.
In a few materials, there is an atomic resonance whose frequency falls within the frequency range of visible light. Senior Michael Zellner wanted to study this effect for his senior seminar project. Dr. Miziumski suggested a solution of potassium permanganate (KMn04) in water as the dispersing medium and Mr. Zellner was on his way.
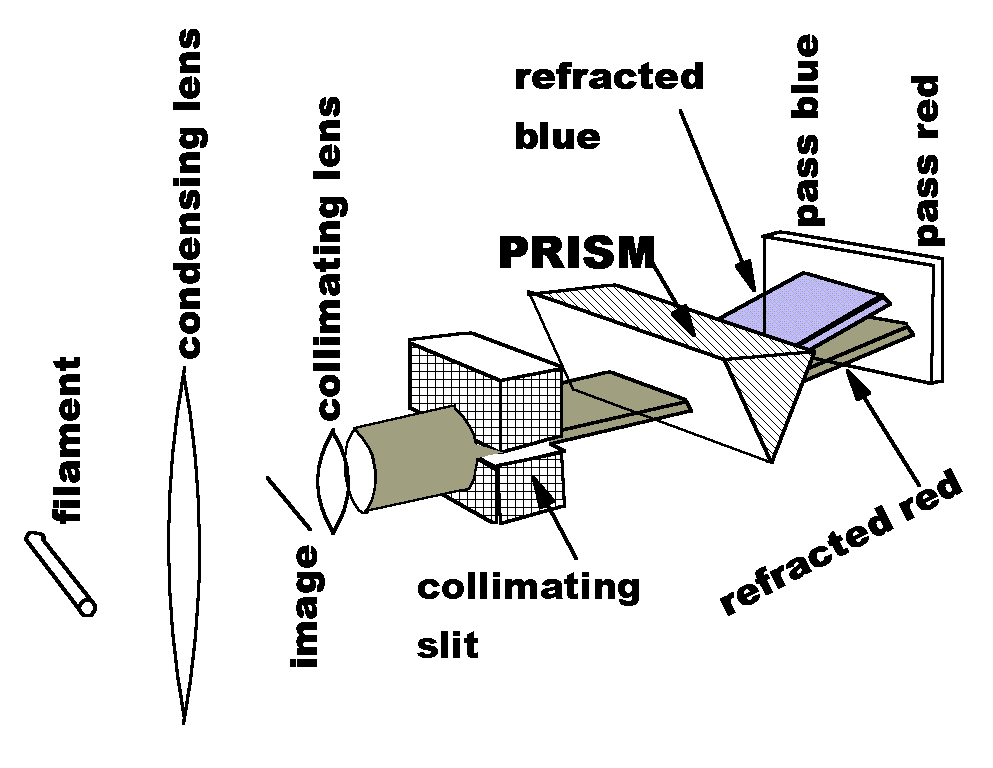
As a theoretical basis, Mike worked through the classical derivation in the book Optics, by Born and Wolf (a classic in itself). For his experiment, he used a hollow prism filled with (KMn04) solution and the apparatus sketched at the right.
White light is generated by the filament of a 500 watt incandescent lamp. A condensing lens gathers much of this light and forms a small image of the filament. A collimating lens, with its focus on the image, produces a beam of parallel rays, roughly the same diameter as the lens.
This cylinder of light is converted to a sheet of light by a collimating slit. The sheet of light enters the prism and is refracted as shown. When water alone is in the prism, the light exits the prism in the usual (vertical) rainbow pattern.
In Mr. Zellner's experiment, the refracted light is passed through a spectral filter. This thin film filter allows blue wavelengths to pass on one end. The thickness of the film increases along the length of the filter, so that increasingly long wavelengths are allowed to pass. Red light passes through the end farthest from the blue-pass region.
For normal dispersion in water, blue wavelengths are refracted through a greater angle, and thus strike the filter at a higher point. This happens for the whole length of the filter, but the blue light is allowed through only at the right end of the figure at right. In this way, the refraction for each wavelength can be displayed in graphical form.
The expected curve for anomalous dispersion is shown, with the resonance approximately in the yellow-green region of the spectrum.
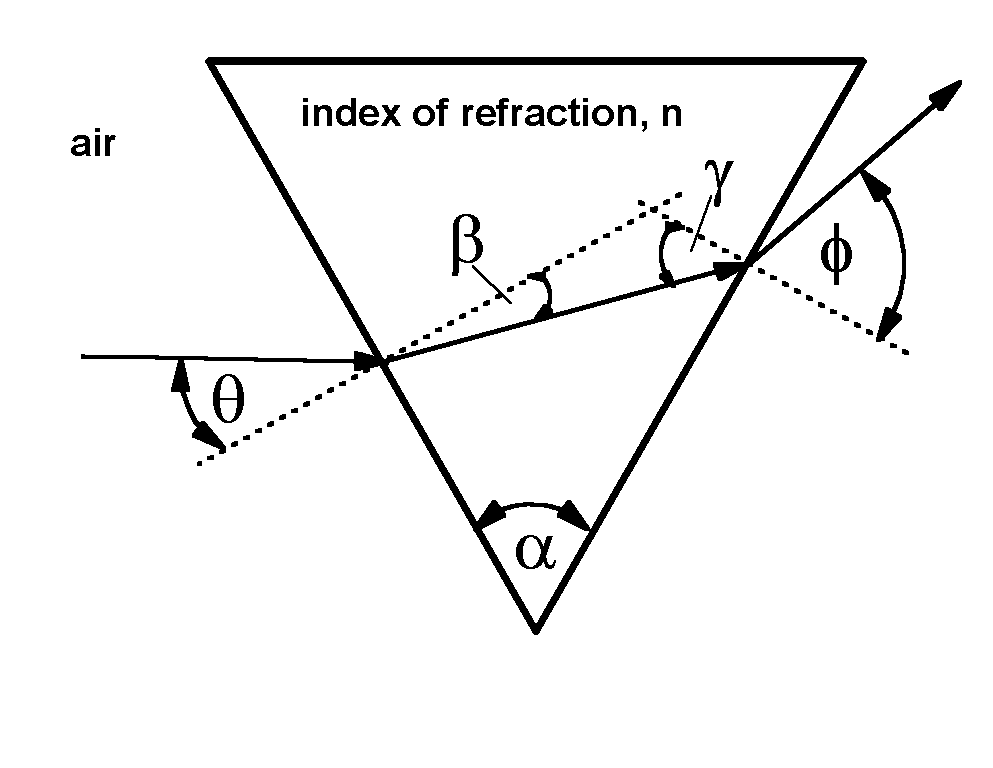
The angle at which the light is refracted is related to the index of refraction and the prism geometry by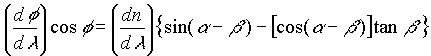 where l is the light wavelength.
where l is the light wavelength.
For water, the index of refraction changes by less than 1% throughout the visible range of wavelengths, so that the angles are nearly constant. In that case it is a good approximation to say that the change of exit angle, f, is proportional to the change in index of refraction, for a given change in wavelength.
The change in f, in turn is proportional to the change in position at which the exiting ray of light hits the spectral filter. Thus the location of the light upon the filter is a fair representation of the index of refraction.

The results of the experiment are displayed photographically. Above is the light passing the filter for pure water. The graph trends upward, with slightly increasing slope. Below is the display for a 4% KMn04 solution.