Experiment of The Month

Our labs do not have written instructions. In keeping with this spirit, the description given here will be brief and general. The intent is that each performance of the lab will be unique; in each nature will reveal a slightly different face to the observer.

This experiment is a favorite of Dr. Price. It uses a nice bit of mathematics called the "parallel axis theorem" in the analysis of the mechanics of the experiment.

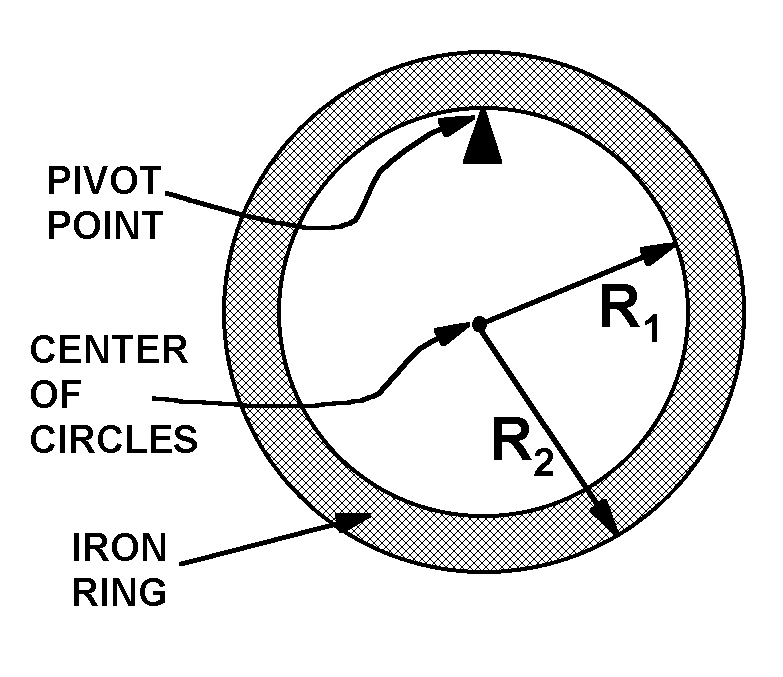
The set-up is shown in the figure at the right. A circular ring of iron is suspended from a pivot (made from a piece of angle iron, clamped to a lab bench). The radii of the inner and outer surfaces of the ring are shown.

The center of the two circles that mark the inner and outer edges of the ring is also the center of mass of the ring. This is a nice example of a system in which there is no actual mass at the center of mass.

In the experiment, the ring is pulled to one side and released. It swings back and forth like a pendulum and students can measure the period of oscillation. The measured period is compared to the period predicted by analysis. As with the simple pendulum, the result is independent of the mass of the pendulum. However, the period now depends on two distances rather than the simple length in the simple pendulum.

The parameters in the analysis are the mass,M, of the ring, the radii shown in the figure above, and the angle shown in the figure at the right

(Note: If your web browser does not support Greek letters, the angle theta will appear as a q, and the angular acceleration alpha will appear as an a.)

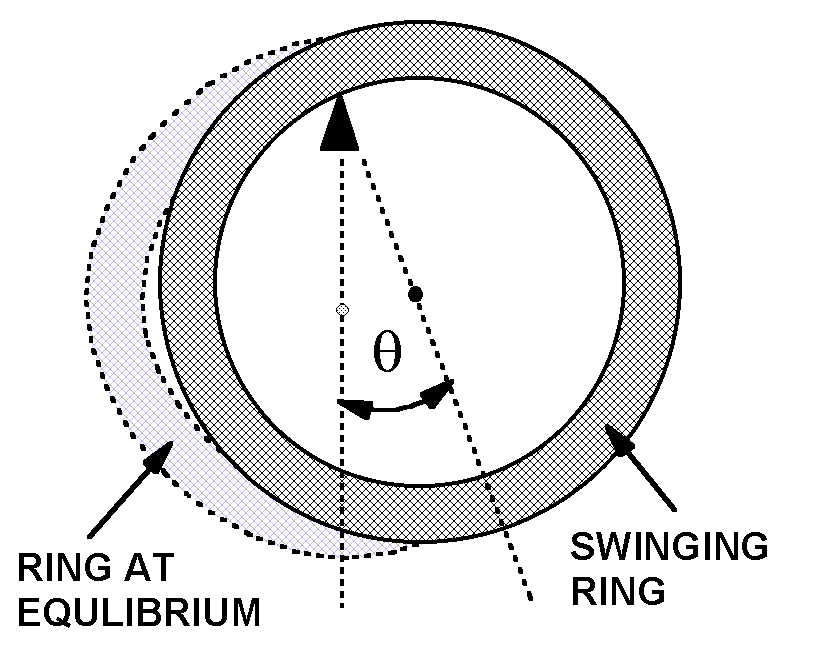
The angle q is formed by two lines, both terminating at the pivot point. The vertical line goes through the center of mass when the pendulum is at equilibrium. The other line goes through the center of mass when the pendulum is displaced from equilibrium.

As usual, the gravitational torque about the pivot point is -MgR₁sinq , with the - sign indicating torque pulling the system back to equilibrium. In the rotational version of Newton's second law, we make the usual small angle approximation and find

-MgR₁q = I a

which leads to an angular frequency, w, given by

w² = (MgR₁ )/I

where I is the moment of inertial of the ring, when the pivot point is as shown in the first figure.

The moment of inertia of the ring about the center of mass is shown to be
(M/2)(R₁² +R₂²)
and the parallel axis theorem gives us

I = MR₁² + (M/2)(R₁² +R₂²) so that

w² = (2gR₁ )/(3R₁² +R₂²)

We note that for a hoop, with the two radii essentially equal, this reduces to

w² = g/(2R₁)

which is the same as a simple pendulum with all its mass at the bottom of the ring.

This exercise can be done with high precision. On occasion we have tried to understand disagreements between measurement and prediction in terms of the pivot being, not a point, but a cylinder of small radius.