Experiment of The Month

Senior Harry Nash decided to study the surface of a rotating fluid. He started by shining light down on the surface of the rotating sample of fluid. He verified the focusing power of the parabolic surface shape. Then at his the suggestion of his advisor (Dr. Miziumski) he tried making a two-component fluid: low density oil floating on top of higher density water. The apparatus is shown in the figure at the right.

The yellow oil floats on top of clear water in a large graduated cylinder, diameter about 6cm. The cylinder sits on a platform which can be rotated, by hand.

The rotatable cylinder, at rest

 

Close view of the oil surface, when the cylinder rotates at about 1 revolution per second. A slight parabolic dish, lower in the center, describes the surface of the oil.

The surprise came when Mr. Nash first began to spin the rotating stage up to speed, while watching the interface between the oil and the water. He saw the effect pictured below:

Spinning cylinder with small paraboloid on top of oil
and large "wrong way" bulge in the oil-water
interface.

 

Close-up of the upward bulge in the oil-water interface. Some structure in the surface is also visible. Harry found that if he kept the cylinder spinning, eventually the interface "returned to normal," taking the expected downward bulging shape. The "wrong-way" bulge is a transient. For some projects the transient nature of the bulge might justify simply ignoring it. However, the fun part of physics is discovering - and then understanding - mysteries, so the project was refocused on this mysterious "wrong way" bulge

Eventually he and Dr. Miziumski developed a simplified version of events which includes the "wrong way" bulge as a natural consequence.

The obvious difference between the oil and the water is that the oil is lower density. That (plus the immiscibility of oil and water) leads to the stratification of the fluid column, with oil on top. In addition, the oil is much more viscous than the water, and this turns out to be crucial to understanding the observed transient effect.

When you begin to spin the rotating stage, the glass column follows the spin immediately, but the fluid inside does not. Oil touching the walls of the column follows quickly. That oil pulls its inner neighbors (nearer the center of the column) and eventually speeds those neighbors up. These neighbors pull on their inner neighbors, speeding them up, and so on, until all the oil is rotating at the same rate as the glass and the stage. In practice, it takes about half a minute to bring all the oil up to rotational speed, about 6 radians per second in our experiment.

The water column speeds up in the same way, but it takes more than a full minute for it to get up to speed.

The force with which a moving liquid pulls on its neighbors is called the viscous force. The strength of the coupling between a bit of moving fluid and its neighbor is called the viscosity of the fluid. Among ordinary fluids, water has low viscosity and sugar syrup has high viscosity. The viscosity of oil is significantly higher than water, and thus spins up more quickly in this experiment.

To understand the phenomenon, Nash and Miziumski simplified to the extreme: They considered the case in which the oil rotated at a uniform rate, and the water did not rotate at all. In the Macroscopic Physics course, (Physics 334) students learn that the pressure in a rotating cylinder of water is given by

P = P₀ + (R/2)(w² r² -2gh)

where P₀ is a reference pressure, R is the density of the fluid, w is the angular velocity, r is the distance of the point of observation from the axis of rotation (the axis of the cylinder, and h is the distance of the point of observation above the bottom of the cylinder.

This tells us that the height, h, of a surface of constant pressure is parabolic; quadratic in r with a constant of proportionality determined by the angular velocity.

If the angular velocity is zero, then the height of a surface of constant pressure is constant; the surface is horizontal. Surfaces like these are sketched below, for the two left examples. Note that the surfaces are separated by a larger distance for the lower-density oil.

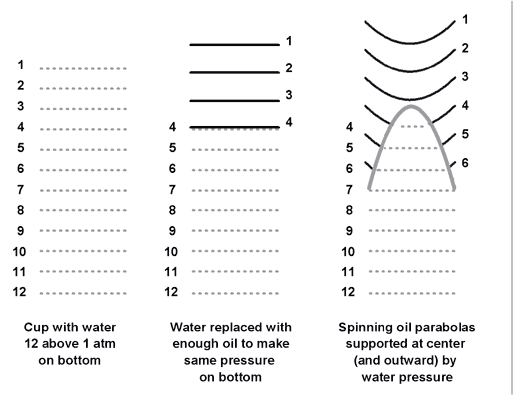
When the oil rotates (and water does not) a surface of constant pressure in oil is a parabola, while a surface of constant pressure in water remains the same. Where the oil and water meet, the pressure must be single valued, so the surfaces must merge, as sketched in the far right part of the figure above.

When the parabolic oil surfaces meet the horizontal water surfaces, the interface between oil and water must adjust so that the pressures match. The surface is indicated with the wide gray line on the right part of the figure above.

We can also think algebraically using the equation for pressure. At a given distance from the axis of rotation, as our point of observation is moved in a vertical direction, the pressure increases with increasing height above the bottom.

Let h1 be the height of the water column at some value of r, and h2 be the height of the oil column above the same water column. The sum of the two is the total distance, D from the bottom of the cylinder to the top surface of the oil.
h1 + h2 = D
Also for this water column, the pressure difference between the top surface and the bottom of the cylinder is given by
R1 g h1 +R1 g h2 = PG
where PG is the gauge pressure at the bottom of the cylinder, and R1, R2 are the two fluid densities.

Combining these two to eliminate h2, we can find the height of the oil-water interface, h1:
h1 = {PG /g - R2 D}/{R1 - R2}

The numerator has a constant term, minus a term proportional to D, which increases parabolically with increasing r from the center of the cylinder. Thus h1 must decrease as we move our observation point from the axis of the cylinder towards the wall of the cylinder.

Because the denominator can be quite small (when the two densities are similar) the variation in h1 can be much larger than the parabolic variation of the top surface of the oil. The upward bulge can be very large, as seen in the figure above.

The figure below at the left shows yet another surprising result.

Before the picture on the left was taken the entire system was rotating, and the rotating table was allowed to slow down. The observed dish in the water surface is much deeper than that observed on the top of the oil surface.

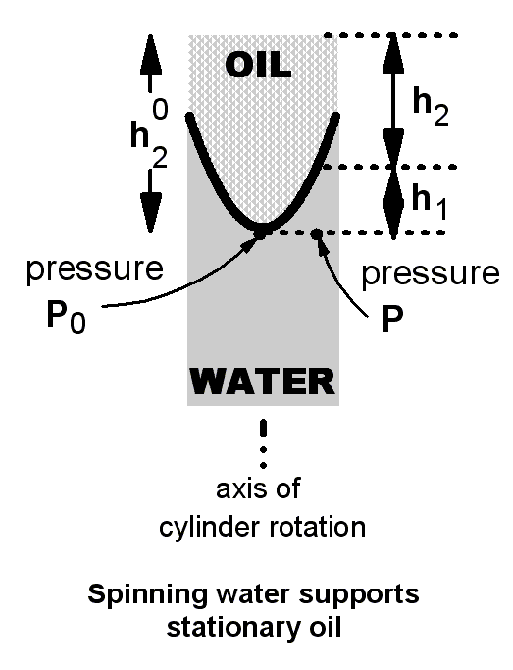
In the same spirit as Nash and Miziumski, we now try a model in which the oil has stopped rotating, but the water is still rotating. As before, the lag in the water response to changing rotation of the cylinder is due to its low viscosity. This model is illustrated on the right above.

Now the surfaces of constant pressure in the oil are horizontal planes, and the surfaces of constant pressure in the water are paraboloids. We are interested in the pressure variation along the lowest dotted line; the horizontal line which passes through the points marked P₀ and P.

The pressure P is related to P₀ by
P = P₀ + a r²
where a is a constant proportional to the rotation rate, and r is the distance of the point of observation from the axis of rotation. (This increase in pressure with r is required to produce the net force needed for the centripetal acceleration of the rotating water at a distance r from the axis.)

The pressure P₀ can be calculated in terms of the density of the oil alone, since only oil sits above that point in the picture:
P₀ = 1 atmosphere + R2 g (h1 + h2)

The pressure P can also be calculated using the column of water and oil above it:
P = 1 atmosphere + R2 g h2 + R1 g h1

The important difference in this expression is the appearance of the two different densities. Equating the two different expressions for the pressure P, we can solve for h1, finding
h1 = {a r²}/{g[R1 - R2]}

If the fluid above the water were air, with density R2 approximately zero, we get the usual parabolic shape to the water-air interface. However, when the fluid above is oil, with a larger density R2, the denominator of the expression becomes small, and the height of the interface, h1, varies much more strongly with r. The simple model does get to the observation of deeper dish than expected for the oil-water interface.