Experiment of The Month

One of our early physics 2 laboratories introduces the oscilloscope by measuring the potential difference, the "voltage," across assemblies of 9V batteries. Part of the appeal is the familiarity of a voltage designation for batteries. A problem is that "voltage" seems like a completely separate idea. It turns out that, although electrical effects certainly involve new physics, there is a natural connection between voltage and our earlier mechanics studies. The connection between the idea of voltage and the idea of mechanical potential is the point of the demonstration described here.

The measuring device is our best voltmeter. The device, called an electrometer, has very high input impedance so that it draws practically no current while measuring a potential difference up to 100 volts. At 10¹⁴ Ohms, it is at least a million times better than typical voltmeters. In the photograph, the electrometers is connected to two metal plates, one plate above the other, so that it measures the electrical potential difference between the plates.

Thin plastic sheets in the gap between the plates ensure that they never touch. A 9 volt battery is used to establish a 9 volt potential difference between the two plates. The upper plate is fixed in position. The lower plate can be moved vertically, so that the gap between the plates changes.

The electric field between the two oppositely charged plates is mostly vertical and mostly uniform. We follow tradition and take it to be uniform and vertical. Staying with this simple model, we take the electric field due to the upper plate to be uniform and vertical. The charge on the lower plate experiences an upward force due to the field of the lower plate.

In the demonstration, the battery is removed after moves charge from bottom to top and establishes the 9 volt potential difference. The charges remain on the plates; the top plate positive and the bottom negative.

If the position of the lower plate is changed, the electric force on it does work. The amount of work done by the electric field has the same magnitude as the change in electrical potential energy of the system. With uniform electric field, the work done (and the change in electrical potential energy) is proportional to the distance moved by the lower plate. If the distance between plates is increased, the work by the electric field is negative, so that the change in electrical potential energy is positive.

As usual, it is up to us to choose the situation which has zero potential energy. It is natural to identify zero potential energy with zero separation between the plates. Then the electrical potential energy is proportional to the separation of the plates.

Now it is time to recall the formal definition of electrical potential as electrical potential energy per unit charge. Since in this demonstration the battery is removed after establishing the 9V potential difference between the plates, the charge on each plate remains constant. As a result, the electrical potential energy is simply proportional to the electric potential (the "voltage").

Following this reasoning, the reading on the voltmeter should be proportional to the separation of the plates. To test this assertion, we start with a narrow gap, at 9V, and lower the bottom plate by lowering the laboratory jack, while measuring the potential difference between the plates. In this demonstration, the electrometer is set to measure 100 volts, full scale.

We made a video recording of the demonstration. A sequence of stills from a second run of the demonstration is shown below.

A graph of potential versus plate separation shows agreement with expectations for small separation. (The first three data points fall on a nice straight line.)

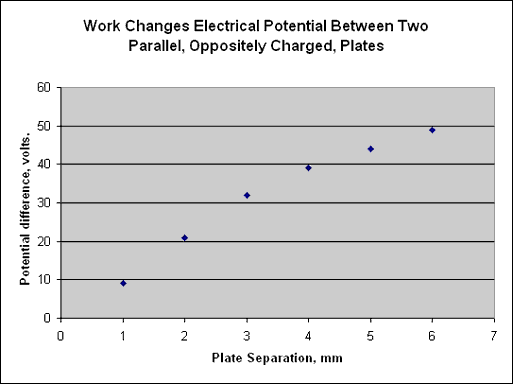
At large separation, the approximation that the field is uniform begins to fail. (It only works for plates which are "large" compared to the size of the gap between them.) For very large separations, we expect the field to fall in accordance with Coulomb's law. This means that for large separations, less work is done to pull the plates apart. In turn, the change in potential energy and in the potential is smaller as we move through larger separations.

A second reason for the "fall off" in the graph at high potential is our relatively high humidity. This leads to flow of charge through the air when potential differences become large. It takes only a minute for the potential to fall by half under the conditions of this demonstration.