Experiment of The Month

John Gentile studied the bounce of a spinning ball experimentally and theoretically, under the guidance of Dr. Nolan. His clearest results were obtained for a ball with "backspin;" The lower part of the ball had larger velocity (in the laboratory frame of reference) than the top part.

Mr. Gentile learned to produce this spin by pulling a board out from underneath the ball, as in the picture. He learned to analyze the bounce using conservation of linear momentum and angular momentum (about the point of contact). He considered two cases:

1. The ball slips along the floor during the collision and
2. The ball does not slip during the collision.

The high speed camera in the foreground was running at 250 frames per second. From observation of the images, it seemed clear that (for the back-spinning ball) the ball did not slip when it hit.

The results of Mr. Gentile's analysis predicted the final ball velocity vector, and its spin, in terms of the initial velocity and spin. The prediction can be written in the form of a matrix, shown below.

The coefficients of 5/7 and 2/7 result from an analysis of the linear and angular momentum conservation laws. The moment of inertia for a solid sphere (I = 2/5 mr²) enters into the calculation in a natural way and determines the numerical coefficients. Interestingly, if a hollow sphere (I = 2/3mr²), like a basketball, were used, then different numerical coefficients would result. The 5/7 becomes 3/5 and the 2/7 becomes 2/5.

The column vector on the left has the x (horizontal) and y (vertical) components of the final velocity vector, in ordinary notation. The z component of the angular velocity is represented in terms of the angular velocity of the ball, omega, and the radius of the ball.

The column vector on the far right represents the initial velocity components. The matrix that couples the two is the result of Mr. Gentile's work. In the matrix, epsilon is the restitution coefficient for the ball. Mr Gentile determined it with separate experiments, dropping the ball vertically with no spin, and measuring the rebound height.

 

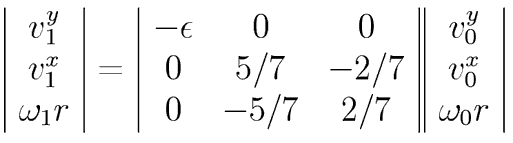
The animated gif file shows every other frame, at an effective rate of 125 frames per second.

In the movie you can see the ball spinning clockwise as it falls, and then as a result of the collision, spinning counter-clockwise as it rises.