Experiment of The Month

The uncertainty principle is associated with waves of any kind. For momentum in the x direction, it states that
Dp Dx= h/(2p)
where Dp is the uncertainty in momentum and Dx is the uncertainty in position.

Squeezing down the uncertainty in position results in an increase in uncertainty in momentum. In this experiment, photons from a laser are passed through the jaws of a caliper. The caliper jaws are moved closer together until just a fraction of the light beam passes through. Now we know the position of the beam (in the x direction, between the jaws) very accurately. The uncertainty principle tells us that the uncertainty in the x component of the photon momentum must be large after passing through the jaws.

The light beam shines on a screen several meters away. The pattern on the screen is the familiar single slit diffraction pattern. The beam is spread out sideways because the x component of momentum is no longer well defined. The x component of photon momentum is uncertain, and this causes uncertainty in where it will land on the screen. In this way, the uncertainty principle is associated with the width of the central maximum of the diffraction pattern.

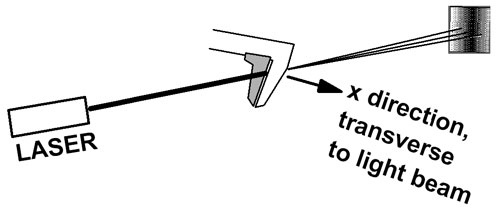
In short, the light entering the caliper jaws had a well-defined momentum vector. (See below for a discussion of radiation pressure and light momentum.) The light leaving the caliper jaws evidently has a variety of momentum vector directions, spread to the right and left about the direction of the original beam.

The uncertainty principle is given in terms of the standard deviation of the momentum distribution, Dp, and the standard deviation of the position distribution, Dx for multiple measurements of the momentum and position of a particle. In this case we think of the particle as a photon. for the position we set Dx = a/2, where a is the width of the opening between the caliper jaws.

For Dp we use the idea that two thirds of the photons lie within one standard deviation of the center of the diffraction pattern. That is, two thirds of the total intensity lies within one standard deviation of the center of the pattern. The formula for the intensity, I, as a function of the deviation angle, q, and the wavelength, l, is (from the Wikipedia article on diffraction).

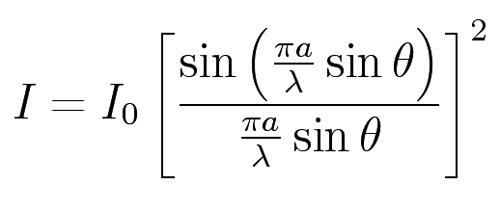
To find the angle which contains 2/3 of the area under this curve, a spreadsheet was used to do a simple integration.

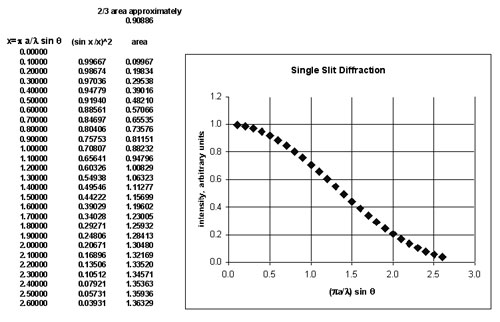
2/3 of the area is contained when the horizontal axis has value about 1.0. At this point, sin q = l/(pa) . A photon which deviates to this value of q has acquired a transverse component of momentum Dp which directs the photon trajectory along the angle q. It is approximately true that

Dp/p= sin q = l/(pa)

Since Dx = a/2, and p=h/ l this leads to

Dp Dx= h/(2p)

as stated in the quantum uncertainty principle.

Radiation Pressure

The figure below shows an electromagnetic plane wave striking a perfectly absorbing Ohmic medium. An Ohmic medium obeys Ohm's law, and the charges move in phase with the applied electric field. The electric field (solid line) oscillates vertically and the magnetic field (dotted line) oscillates in a plane perpendicular to the page, as shown.

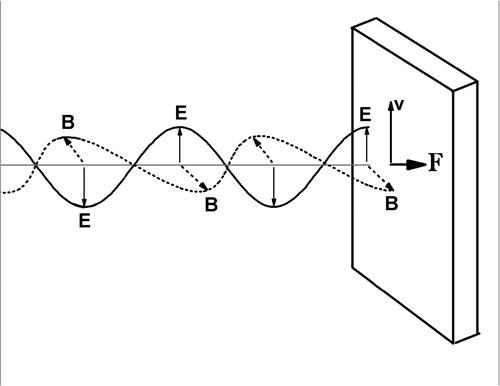
The velocity of a positive charge is in phase with the electric field, and in the same direction as the electric field. The magnetic field exerts a force on this charge, F=qv x B in the same direction as the propagation direction of the wave. This force can be used to calculate the radiation pressure on the medium. In this case we ask about the momentum transferred to the medium, related to the force by F = dp/dt.

We can also calculate the work done in a time dt by the electric field as qEvdt. (The magnetic force does no work.) Using the fact that (for an electromagnetic wave) E=B/c where c is the speed of light, we can calculate the momentum delivered (dp = qvB dt) when an amount of energy equal to the energy of one photon (hf) is absorbed by the medium. The result is that p = h/ l.