Experiment of The Month

For his senior seminar project, Tim Dennis decided to determine experimentally whether a water sprinkler would turn backwards if the water flow were reversed. His apparatus used the siphon flow method described on the University of Maryland website. His apparatus did not use a rotating water sprinkler, but a single right-angle nozzle, similar to that discussed by Jenkins in the American Journal of Physics. For more siphon information click here.

In the picture, Tim is observing the flow pattern in the surrounding water, which has been decorated with lycopodium powder.

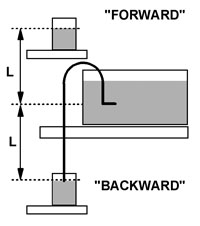
The siphon set-up is shown above, right. In the figure, water flows "forward" from the top reservoir, through the nozzle and squirts to the right into the large tank. The vertical leg of the nozzle is flexible. When water flows "forward" into the tank, the vertical leg flexes, and the nozzle "reoils" to the left, as expected.

If this were a water sprinkler, the sprinkler would turn clockwise when viewed as in the figure.

When the reservoir is moved down so that the siphon runs the other way, with the same drop, L, water flows "backwards" from the large tank into the lower reservoir at roughly the same rate.

Tim observed that the nozzle "recoils" to the right when the water flows "backwards" to the left. This agrees with the observations at the University of Maryland.

In the two figures below, water flow is shown for both situations, "forward" on the left and "backward" on the right.

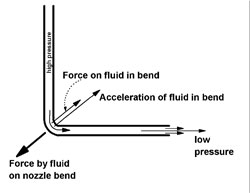
Dr. Miziumski, Tim's seminar advisor, showed him that the force at the bend in the "forward" direction is easy to understand from the curved path that fluid must follow in the elbow of the nozzle. The centripetal acceleration and the force on the fluid point towards the center of the fluid path. The third law tells us the direction of the force by the fluid on the nozzle.

Dr. Miziumski pointed out that this means that the force by the fluid on the bend is exactly the same for fluid flowing at the same rate but "backward." Ignoring viscosity, if there is a difference in the behavior of the nozzle it must be caused by fluid outside the nozzle.

When fluid is flowing in the "forward" direction, fluid exits to the right. In a time Dt, fluid with mass Dm = r (p R2 vo Dt) is expelled, where r is the fluid density, R is the radius of the nozzle opening, and vo is the velocity of fluid at the tip.

During the Dt, this fluid carries away momentum
Dp = Dm vo = r (p R² v_o² Dt) .
The recoil force is dp/dt so
(recoil force) = rp R_² v_o²
for the "forward" direction of flow.

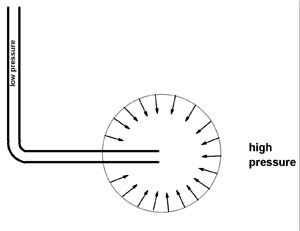
Dr. Miziumski suggested to Tim that in the "backward" flow condition, the nozzle might be approximated as a sink for fluid. For a sink, the fluid would flow in a spherically symmetric pattern towards the sink. To a first approximation, the inward flow would be the same across each part of the sphere in the figure at the right.

If the nozzle blocked nothing, then the momentum flowing across the sphere adds to zero. No momentum is delivered to the nozzle; the nozzle feels no force, and does not recoil. With the nozzle blocking some of the flow, this dynamical effect would produce a net force to the left on the nozzle. The dynamical effect pushes the nozzle back in the same direction as the recoil for "forward" flow, although not as strongly.

The nicest feature of this point of view is that only forces external to the nozzle need be considered. The sink model is only approximately correct, because fluid flowing from most directions must curl in order to enter the tube. A true sink requires no curl.

To imagine a mechanism that produces a force to the left when the nozzle runs "backwards," it helps to remember the mechanism of the siphon. The siphon does not depend on atmospheric pressure. The weight of the water on the downward straight leg of the siphon produces a tension in the water which draws water into the nozzle. (This tensile force is often associated with the surface tension.)

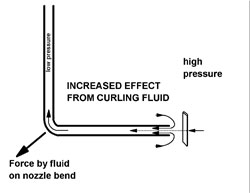
The figure below, left, shows fluid curling into the nozzle. This path requires a centripetal acceleration, with a force towards the center of the circular path, roughly towards the middle of the nozzle. This force requires a pressure gradient, with low pressure near the nozzle and high pressure further away. If the distant, higher, pressure is the same as the ambient pressure at the level of the nozzle, then the nozzle experiences a pressure gradient increasing to the left, and a consequent force to the right.

A similar effect was discussed for the aspirator in the previous experiment of the month. In this case, the low pressure near the mouth of the nozzle is provided by the tension in the water, caused by the siphon action.

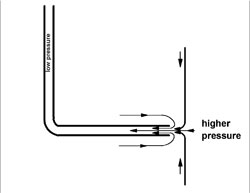
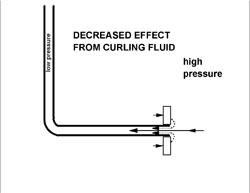
The significance of the fluid curling into the nozzle from the left can be tested by blocking the flow as suggested above, right. If we block the curling flow, directed along the axis into the nozzle, then the net rightward force on the nozzle should decrease. Blocking the curling flow should decrease the net rightward force on the nozzle.