Experiment of The Month
Relation of Bending Moment to Maximum Tensile Stress
When a beam is bent, the outer edges of the bend experience the greatest tensile stress. This stress is related to the bending moment, M, the distance from the center of the beam (technically the centroid) to the outer edge, c, and the "moment of inertia" of the beam
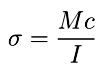 where I is calculated as
where I is calculated as

To arrive at this, consider two images of a bending beam:
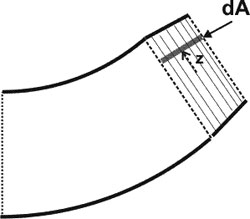 |
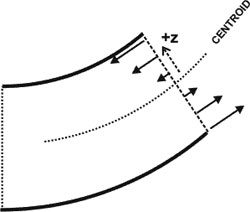 |
|
Side view of a beam being bent by force pairs |
3-D view showing the beam cross section for the I integral |
The left figure shows the forces that are assumed to be in play when we cause a bend in the beam. They produce a torque about the centroid. Forces on the inner half of the bend act to compress and forces on the outer half act to stretch.
The outermost edge must force all of the interior material to flex, so the outermost force must be the largest in magnitude. We assume, with Mott (Applied Strength of Materials) that a plane cross section of the beam remains plane when the beam is bent. This requires uniformly increasing force from the centroid to the outer edge. The arrows indicate the forces, which obey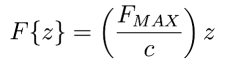
The force can be written in terms of the tensile stress:
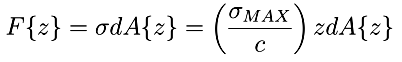
The moment (torque) applied to the cross section is the sum of all the moments:
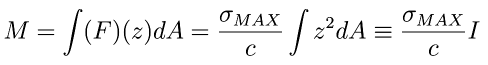
This is solved for the maximum stress:
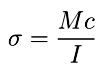
-
Contact Information
Contact Number: 717-871-4297
Email: physics@millersville.edu