Experiment of The Month

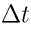
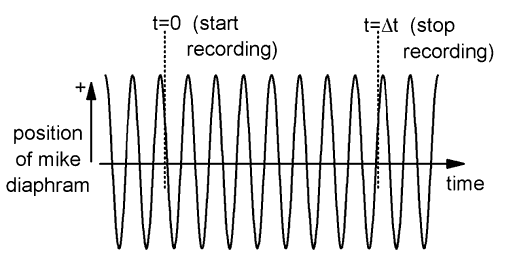
If we record a tone with frequency f for a period of time , we can determine the frequency by counting the number of cycles in the record.

In the figure, we would count seven peaks during the interval 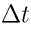so the frequency would be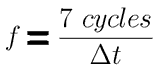

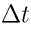If happens to be 1 second, then the frequency is

.

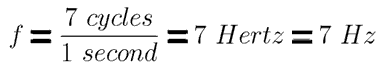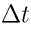
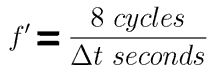
If we had started or ended our interval a little later or a little earlier, we would probably have counted 8 cycles instead of 7. This would give a different frequency:.

It is fair to say that our value for the frequency is uncertain, and the size of the uncertainty is 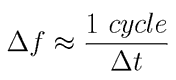about . When discussing this uncertainty, most people multiply both sides by and drop the word "cycle" to get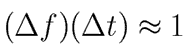

Physicists call this sort of equation an "uncertainty principle." We are interested in it because it applies in a variety of places, meaning (for example) that if you measure the energy of a particle for a short time then you cannot have an accurate result for the energy (no matter how good your instruments are).

The longer you spend measuring the frequency, the smaller is your uncertainty. (The idea is that you are always uncertain by about 1 cycle, but this doesn't make much difference if you counted a lot of cycles - just as a dollar difference in price is important for a hamburger but not for a car.)

In many things, like a pendulum, the vibration dies away soon after you stop adding energy. (Think of playing a clarinet - the sound stops almost immediately after you stop blowing.) In these cases, the is not determined by how long you record the vibration, but by how long the vibration lasts. Then the uncertainty in frequency (of the pendulum for example) is given by

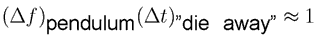
For a solid iron 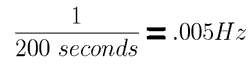pendulum the vibration lasts a long time. For a tennis ball pendulum, (with length of about1 \ meter) the vibration dies down within about 3 minutes - say 200 seconds. The uncertainty principle predicts an uncertainty of about

Using a formula for the frequency of a pendulum, this corresponds to an uncertainty of about 1cm in the 1 meter pendulum length.

In the figure from past experiment 80, the four tennis balls that respond most strongly to the heavy driver pendulum vary in length by about 1cm, from the longest to the shortest. In an ideal case, the only pendulum that would respond to the driver would be the one with exactly the same length. That is it would be nearly impossible to construct a pendulum that would respond.

Because there is uncertainty in the frequency of the tennis ball pendulum, the driver is able to drive a tennis ball of the "wrong" length. Essentially, the tennis ball "forgets" what it was doing 200 seconds ago, so even if the driver was "out of step" then, the fact is forgotten, and the tennis ball accepts energy from the driver.

Because it "forgets", the tennis ball swings in sympathy with the current driver oscillation, at the current driver frequency.

The uncertainty in the frequency is often called the width of the oscillating object. A driver with a frequency with the range defined by the width will successfully couple to the oscillator. The oscillator with a large width (short "lifetime") is able to accept energy from drivers over a wide range of frequencies.

In quantum mechanics, the frequency is connected to the energy of an object, and the same relation predicts that an object can have a very large (comparable to its rest energy mc²) for a time interval of very short duration. It is for this reason that empty space is said to be "frothy" over short time intervals.