Experiment of The Month

Three senior physics majors, Cody Borigo, Kevin Dougherty, and Darren Scott, are taking a special topics course in Strength of Materials, a standard course for mechanical engineering students. They intend to use the material as they pursue graduate degrees in mechanical engineering. As a break from working through the text (Applied Strength of Materials by R.L. Mott) they did a laboratory experiment to test one of the fundamental equations used to analyze the bending of beams:

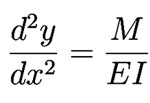
where y is the displacement shown in the figure, and x is the displacement in the figure, measured from the orange clamp at the bottom. M is the bending moment (torque) experienced by the beam at the location x. E is the Young's modulus, and I is called the "moment of area," or (incorrectly, but commonly enough that everyone understands) the "moment of inertia."

where the integral is over the cross sectional area of the beam. (If dA were an element of mass this would be a moment of inertia.)

The differential equation predicts that when a beam is clamped (with the orange clamp) and pulled at its other end (with the black paper clip, as in the figure below, the deflection (y) of the beam as a function of distance from the clamp (x) is:

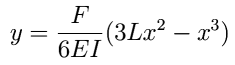
where F is the applied force (measured with the spring balance shown and later with an electronic force probe) and L is the length of the beam (in this case almost two meters).

The particular experiment shown uses two 2-meter sticks side by side. The moment of inertia in this case is:

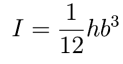
where h is the height of the two stacked sticks, and b is the thickness, measured in the direction of y.

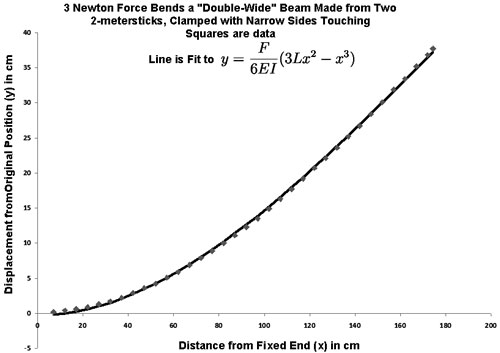
Cody, Kevin, and Darren applied a 3 Newton force to the end of the beam and traced the shape of the distorted beam on paper, producing a line as shown in the figure at the right. They also traced the figure of the beam when no force was applied.

They then measured the y distance from the un-stressed line and used Excel's "solver" function to fit the formula to the data. In the fit, the quantity

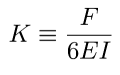
was taken as an adjustable parameter, and a small (0.24cm) constant term was added to account for a small y offset. The fit is shown below. The standard deviation between the experimental value of y and the fit is 0.25 cm, leading us to estimate the uncertainty in K at about 1%. With this estimate, we find

 

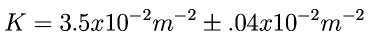
For the double-wide setup shown in the figure, the moment of inertia was calculated from the measured dimensions of the meter sticks to be

 

This led to an estimate for the Young's modulus for the wood of

 

E for red maple is listed as 1.13x10 10 Pa

Interestingly, when the sticks were clamped with wide sides together, the agreement was poor. This is presumably because the sticks are not welded together and the assumption that a cross section of the composite beam is undistorted by the bending fails. In fact we could see visually that the stick markings shifted relative to each other upon bending. (This did not happen when the sticks were bent as in the first figure.)

Bending the "double thick" beam combination

Measuring the y-displacement as a function of x.